
 ���Ӵ�ý��˾Ϊ�˽�ij�������ڶ�ij��������Ŀ����������������ȡ��100�����ڽ��е��飬����Ů����55���������Ǹ��ݵ��������ƵĹ����վ��տ���������Ŀʱ���Ƶ�ʷֲ�ֱ��ͼ�����վ��տ���������Ŀʱ�䲻����40���ӵĹ��ڳ�Ϊ�������ԡ�����֪�������ԡ�����10��Ů�ԣ�
���Ӵ�ý��˾Ϊ�˽�ij�������ڶ�ij��������Ŀ����������������ȡ��100�����ڽ��е��飬����Ů����55���������Ǹ��ݵ��������ƵĹ����վ��տ���������Ŀʱ���Ƶ�ʷֲ�ֱ��ͼ�����վ��տ���������Ŀʱ�䲻����40���ӵĹ��ڳ�Ϊ�������ԡ�����֪�������ԡ�����10��Ů�ԣ�| �������� | ������ | �ϼ� | |
| �� | |||
| Ů | |||
| �ܼ� |
| P��K2��k0�� | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
���� ��1����Ƶ�ʷֲ�ֱ��ͼ�п�֪����ȡ��100�������У��������ԡ����У�0.020+0.005����10��100=25�����ɵ�2��2����������2��2�������е����ݴ��빫ʽ����ɵ�K2�Ĺ۲�ֵΪ��k��3.030���ɡ������Լ������ԭ���������жϳ���
��2����Ƶ�ʷֲ�ֱ��ͼ�п�֪�������������ԡ���5�����Ӷ�һ�п��ܽ������ɵĻ����¼��ռ䦸={��a1��a2������a1��a3������a2��a3������a1��b1������a1��b2������a2��b1������a2��b2������a3��b1������a3��b2������b1��b2��}������ai��i=1��2��3����ʾ���ԣ�bj��j=1��2����ʾŮ�ԣ���A��ʾ�¼����ӡ����������ԡ�������ѡȡ2����������1��Ů�Թ��ڡ����ɵ��¼�A����7�������¼������ùŵ���ʼ��㹫ʽ���ɵó���
��� �⣺��1����Ƶ�ʷֲ�ֱ��ͼ�п�֪����ȡ��100�������У��������ԡ����У�0.020+0.005����10��100=25�����ɵ�2��2��������
| �������� | ������ | �ϼ� | |
| �� | 30 | 15 | 45 |
| Ů | 45 | 10 | 55 |
| �ܼ� | 75 | 25 | 100 |
���� ���⿼���ˡ������Լ������ԭ�������ŵ���ʼ��㹫ʽ��Ƶ�ʷֲ�ֱ��ͼ�������ʣ�������������������������������е��⣮


 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
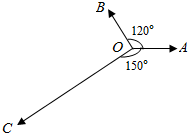 ��ͼ��ʾ��ƽ��������������$\overrightarrow{OA}$��$\overrightarrow{OB}$��$\overrightarrow{OC}$��$\overrightarrow{OA}$��$\overrightarrow{OB}$�н�Ϊ120�㣬$\overrightarrow{OA}$��$\overrightarrow{OC}$�н�Ϊ150�㣬��$|{\overrightarrow{OA}}|=|{\overrightarrow{OB}}|=1$��$|{\overrightarrow{OC}}|=2\sqrt{3}$����$\overrightarrow{OC}=��\overrightarrow{OA}+��\overrightarrow{OB}$���ˣ��̡�R�������+��=��������
��ͼ��ʾ��ƽ��������������$\overrightarrow{OA}$��$\overrightarrow{OB}$��$\overrightarrow{OC}$��$\overrightarrow{OA}$��$\overrightarrow{OB}$�н�Ϊ120�㣬$\overrightarrow{OA}$��$\overrightarrow{OC}$�н�Ϊ150�㣬��$|{\overrightarrow{OA}}|=|{\overrightarrow{OB}}|=1$��$|{\overrightarrow{OC}}|=2\sqrt{3}$����$\overrightarrow{OC}=��\overrightarrow{OA}+��\overrightarrow{OB}$���ˣ��̡�R�������+��=��������| A�� | 1 | B�� | $-\frac{9}{2}$ | C�� | -6 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
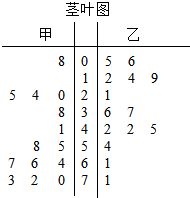 Ϊ�˵���ס���������վ�ܻ�ӭ�ij̶ȣ����ѡȡ��14�죬ͳ������8��00-10��00����Եĵ�������õ���ͼ��Ҷͼ����ס���������վ���������λ���ֱ��ǣ�������
Ϊ�˵���ס���������վ�ܻ�ӭ�ij̶ȣ����ѡȡ��14�죬ͳ������8��00-10��00����Եĵ�������õ���ͼ��Ҷͼ����ס���������վ���������λ���ֱ��ǣ�������| A�� | 55��36 | B�� | 55.5��36.5 | C�� | 56.5��36.5 | D�� | 58��37 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��{\frac{lg2}{2}��\frac{lge}{e}}��$ | B�� | $��{0��\frac{1}{e}}��$ | C�� | $��{\frac{lg2}{2}��e}��$ | D�� | $��{0��\frac{lg2}{2}}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У�C=$\frac{��}{2}$��A=$\frac{��}{3}$����C����ABC�����Բ������CD��BD��CD��BD�����Բ���ڵ�E����DE�ij�Ϊ2����AC=10��
��ͼ���ڡ�ABC�У�C=$\frac{��}{2}$��A=$\frac{��}{3}$����C����ABC�����Բ������CD��BD��CD��BD�����Բ���ڵ�E����DE�ij�Ϊ2����AC=10���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ${a_n}=n+\frac{1}{2^n}$ | B�� | ${a_n}=n•\frac{1}{2^n}$ | C�� | ${a_n}=n+\frac{1}{{{2^{n-1}}}}$ | D�� | ${a_n}=��{n-1}��+\frac{1}{{{2^{n-1}}}}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com