
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且bcosC=(3a﹣c)cosB.D为AC边的中点,且BD=1,则△ABD面积的最大值为 .
【答案】![]()
【解析】解:∵bcosC=(3a﹣c)cosB,
∴利用正弦定理化简得:(3sinA﹣sinC)cosB=sinBcosC,
整理得:3sinAcosB=sinBcosC+cosBsinC=sin(B+C)=sinA,
∵sinA≠0,
∴cosB= ![]() ,可得sinB=
,可得sinB= ![]() ,
,
∵点D为边AC的中点,
∴2 ![]() =
= ![]() +
+ ![]() ,
,
∴两边平方可得:4| ![]() |2=|
|2=| ![]() |2+2|
|2+2| ![]() ||
|| ![]() |cos∠ABC+|
|cos∠ABC+| ![]() |2
|2
设| ![]() |=c,|
|=c,| ![]() |=a,可得:4=a2+c2+
|=a,可得:4=a2+c2+ ![]() ac≥ac,(当且仅当a=c=2时等号成立),
ac≥ac,(当且仅当a=c=2时等号成立),
∴ac≤ ![]() ,(当且仅当a=c=2时等号成立),
,(当且仅当a=c=2时等号成立),
∴S△ABC= ![]() acsin∠ABC≤
acsin∠ABC≤ ![]() ×
× ![]() ×
× ![]() =
= ![]() (当且仅当a=c=2时等号成立),
(当且仅当a=c=2时等号成立),
∴S△ABD= ![]() S△ABC=
S△ABC= ![]() .(当且仅当a=c=2时等号成立),
.(当且仅当a=c=2时等号成立),
∴当且仅当a=c=2时,△ABD面积的最大值为 ![]() .
.
【考点精析】解答此题的关键在于理解正弦定理的定义的相关知识,掌握正弦定理:![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】若将函数y=2sin 2x的图像向左平移 ![]() 个单位长度,则评议后图象的对称轴为( )
个单位长度,则评议后图象的对称轴为( )
A.x= ![]() –
– ![]() (k∈Z)
(k∈Z)
B.x= ![]() +
+ ![]() (k∈Z)
(k∈Z)
C.x= ![]() –
– ![]() (k∈Z)
(k∈Z)
D.x= ![]() +
+ ![]() (k∈Z)
(k∈Z)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,△PAD为正三角形,AB∥CD,AB=2CD,∠BAD=90°,PA⊥CD,E为棱PB的中点 (Ⅰ)求证:平面PAB⊥平面CDE;
(Ⅱ)若直线PC与平面PAD所成角为45°,求二面角A﹣DE﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个集合A,B,满足BA.若对任意的x∈A,存在ai , aj∈B(i≠j),使得x=λ1ai+λ2aj(λ1 , λ2∈{﹣1,0,1}),则称B为A的一个基集.若A={1,2,3,4,5,6,7,8,9,10},则其基集B元素个数的最小值是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的离心率为
的离心率为 ![]() ,M为C上除长轴顶点外的一动点,以M为圆心,
,M为C上除长轴顶点外的一动点,以M为圆心, ![]() 为半径作圆,过原点O作圆M的两条切线,A、B为切点,当M为短轴顶点时∠AOB=
为半径作圆,过原点O作圆M的两条切线,A、B为切点,当M为短轴顶点时∠AOB= ![]() . (Ⅰ)求椭圆的方程;
. (Ⅰ)求椭圆的方程;
(Ⅱ)设椭圆的右焦点为F,过点F作MF的垂线交直线x= ![]() a于N点,判断直线MN与椭圆的位置关系.
a于N点,判断直线MN与椭圆的位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,若这200名学生中每周的自习时间不超过m小时的人数为164,则m的值约为( ) 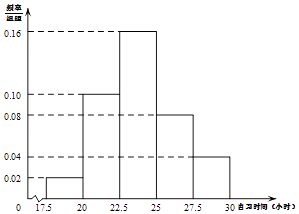
A.26.25
B.26.5
C.26.75
D.27
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=ln(ax+b)+x2(a≠0).
(1)若曲线y=f(x)在点(1,f(1))处的切线方程为y=x,求a,b的值;
(2)若f(x)≤x2+x恒成立,求ab的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com