
【题目】已知函数![]()
![]() 若
若![]() 是函数
是函数![]() 的极值点,1是函数
的极值点,1是函数![]() 的一个零点,求
的一个零点,求![]() 的值;
的值;
![]() 当
当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
![]() 若对任意
若对任意![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立,求实数a的取值范围.
成立,求实数a的取值范围.
【答案】(1)![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]() .
.
【解析】
(1)先求导得到![]() ,由
,由![]() ,
,![]() ,得到
,得到![]() 的值,继而求出
的值,继而求出![]() 的值;
的值;
(2)求出函数的导数,通过讨论![]() 的范围,求出函数的单调区间即可;
的范围,求出函数的单调区间即可;
(3)令![]() ,问题转化为
,问题转化为![]() 上
上![]() 有解即可,亦即只需存在
有解即可,亦即只需存在![]() 使得
使得![]() 即可,连续利用导函数,然后分别对
即可,连续利用导函数,然后分别对![]() ,看是否存在
,看是否存在![]() 使得
使得![]() ,进而得到结论.
,进而得到结论.
(1)![]() ,
,
∵![]() 是函数
是函数![]() 的极值点,
的极值点,
∴![]() .
.
∵1是函数![]() 的零点,得
的零点,得![]() ,
,
由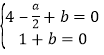 ,
,
解得![]() ,
,![]() ,
,
∴![]() ;
;
(2)![]() 时,
时,![]() ,
,![]() ,
,
![]() ,
,
![]() 时,
时,![]() ,
,![]() 递增,
递增,
![]() 时,令
时,令![]() ,解得:
,解得:![]() ,
,
令![]() ,解得:
,解得:![]() ,
,
故![]() 在
在![]() 递减,在
递减,在![]() 递增;
递增;
(3)令![]() ,
,![]() ,则
,则![]() 为关于
为关于![]() 的一次函数且为增函数,
的一次函数且为增函数,
根据题意,对任意![]() ,都存在
,都存在![]() (
(![]() 为自然对数的底数),使得
为自然对数的底数),使得![]() 成立,
成立,
则在![]() 上
上![]() ,有解,
,有解,
令![]() ,只需存在
,只需存在![]() 使得
使得![]() 即可,
即可,
由于![]() ,
,
令![]() ,
,![]() ,
,![]() ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增,![]() ,
,
①当![]() ,即
,即![]() 时,
时,![]() ,即
,即![]() ,
,![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() ,不符合题意.
,不符合题意.
②当![]() ,即
,即![]() 时,
时,![]() ,
,![]()
若![]() ,则
,则![]() ,所以在
,所以在![]() 上
上![]() 恒成立,即
恒成立,即![]() 恒成立,∴
恒成立,∴![]() 在
在![]() 上单调递减,
上单调递减,
∴存在![]() 使得
使得![]() ,符合题意.
,符合题意.
若![]() ,则
,则![]() ,∴在
,∴在![]() 上一定存在实数
上一定存在实数![]() ,使得
,使得![]() ,
,
∴在![]() 上
上![]() 恒成立,即
恒成立,即![]() 恒成立,∴
恒成立,∴![]() 在
在![]() 上单调递减,
上单调递减,
∴存在![]() 使得
使得![]() ,符合题意.综上所述,当
,符合题意.综上所述,当![]() 时,对任意
时,对任意![]() ,都存在
,都存在![]() (
(![]() 为自然对数的底数),使得
为自然对数的底数),使得![]() 成立.
成立.


科目:高中数学 来源: 题型:
【题目】已知点![]() 与点
与点![]() 在直线
在直线![]() 的两侧,给出以下结论:①
的两侧,给出以下结论:① ![]() ;② 当
;② 当![]() 时,
时,![]() 有最小值,无最大值;③
有最小值,无最大值;③ ![]() ;④ 当
;④ 当![]() 且
且![]() 时,
时,![]() 的取值范围是
的取值范围是![]() ;正确的个数是( )
;正确的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
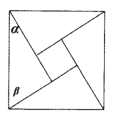
【题目】《周髀算经》中给出了弦图,所谓弦图是由四个全等的直角三角形和中间一个小正方形拼成一个大的正方形,若图中直角三角形两锐角分别为![]() ,
,![]() ,且小正方形与大正方形面积之比为
,且小正方形与大正方形面积之比为![]() ,则
,则![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解儿子身高与其父亲身高的关系,随机调查了5对父子的身高,统计数据如下表所示.
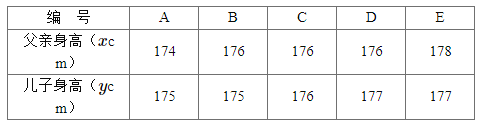
(1)从这五对父子任意选取两对,用编号表示出所有可能取得的结果,并求随机事件M![]() “两对父子中儿子的身高都不低于父亲的身高”发生的概率;
“两对父子中儿子的身高都不低于父亲的身高”发生的概率;
(2)由表中数据,利用“最小二乘法”求![]() 关于
关于![]() 的回归直线的方程.
的回归直线的方程.
参考公式: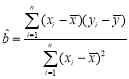 ,
,![]() ;回归直线:
;回归直线:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中“sinA>sinB”是“cosA<cosB”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上恰有一个实数解,求
上恰有一个实数解,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若存在
,若存在![]() 使得函数
使得函数![]() 在区间
在区间![]() 上的最大值和最小值的差不超过1,求
上的最大值和最小值的差不超过1,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com