练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图所示，已知四边形ABCD、EADM和MDCF都是边长为a的正方形，点P、Q分别是ED和AC的中点，求：

    （1）异面直线PM与FQ所成的角；

    （2）四面体P-EFB的体积；

    （3）异面直线PM与FQ的距离．

    答案：
    解析：

    		解：（1）将已知图形以AD、DC、DM为相邻的三条棱补成如图所示的正方体，易知BF∥MP，连结BQ，则ÐQFB即为异面直线PM与FQ所成的角，由正方体的性质知DBFQ是直角三角形，由，知ÐQFB=30°，即所求的为30°；

    （2）由于DP=PE，所以四面体P-EBF的体积等于四面体D-EBF的一半，所以所求的体积；

    （3）由（1）异面直线PM与FQ的距离即为MP到平面BFQ的距离，也即M点到平面BFD的距离，设这一距离为d，

    ∴


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：044

    如图所示，已知四边形ABCD的对角线互相平分，点O是对角线AC与BD的交点．求证：四边形ABCD是平行四边形．

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：044

    如图所示，已知四边形ABCD的对角线互相平分，点O是对角线AC与BD的交点．求证：四边形ABCD是平行四边形．

    查看答案和解析>>

    科目：高中数学 来源：黄冈中学　高一数学(下册)、第五章　平面向量单元(5.1～5.5)测试卷 题型：044

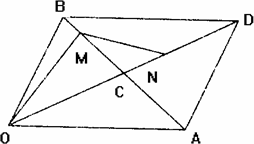
    如图所示，已知四边形OADB是以向量，为边的平行四边形，其中，．试以向量a，b为一组基底，表示出向量、、．

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年江西赣州四所重点中学高三上学期期末联考文数学试卷（解析版） 题型：解答题

    如图所示，已知四边形ABCD是正方形，EA⊥平面ABCD，PD∥EA，AD＝PD＝2EA＝2，F,G,H分别为BP,BE,PC的中点。

    （Ⅰ）求证：平面FGH⊥平面AEB；

    （Ⅱ）在线段PC上是否存在一点M，使PB⊥平面EFM？若存在，求出线段PM的长；若不存在，请说明理由．

     

    查看答案和解析>>

    同步练习册答案