
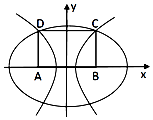
 在平面直角坐标系xOy中,矩形ABCD的一边AB在x轴上,另一边CD在x轴上方,且AB=8,BC=6,其中A(-4,0)、B(4,0).
在平面直角坐标系xOy中,矩形ABCD的一边AB在x轴上,另一边CD在x轴上方,且AB=8,BC=6,其中A(-4,0)、B(4,0).分析 (1)由椭圆的定义:丨CA丨+丨CB丨=16=2a,求得a=8,则b2=a2-c2=64-16=48,即可求得椭圆方程;
(2)根据双曲线的定义:丨CA丨-丨CB丨=4=2a′,则求得a′=2,则b2=c2-a′2=16-4=12,即可求得双曲线的标准方程.
解答 解:(1)∵A、B为椭圆的焦点,且椭圆经过C、D两点,
根据椭圆的定义:丨CA丨+丨CB丨=16=2a,
∴a=8,…4分
在椭圆中:b2=a2-c2=64-16=48,…6分
∴椭圆方程为:$\frac{{x}^{2}}{64}+\frac{{y}^{2}}{48}=1$;…8分
(2)∵A、B为双曲线的焦点,且双曲线经过C、D两点,
根据双曲线的定义:丨CA丨-丨CB丨=4=2a′,
∴a′=2,…10分
在双曲线中:b2=c2-a′2=16-4=12,…12分
∴双曲线方程为:$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{12}=1$.…14分.
点评 本题考查椭圆及双曲线的标准方程,椭圆及双曲线的定义,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $3\sqrt{3}$ | B. | 2$\sqrt{5}$ | C. | $4\sqrt{5}$ | D. | $-4\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
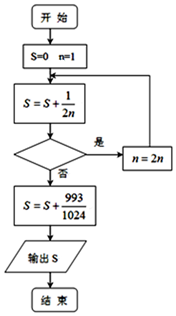
| A. | n<10 | B. | n≤10 | C. | n≤1024 | D. | n<1024 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | $-\frac{1}{5}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=(x+1)2,x∈(0,+∞) | B. | y=log${\;}_{\frac{1}{2}}$x,x∈(1,+∞) | ||
| C. | y=2x-1 | D. | y=$\sqrt{2x-1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 我们把b除a的余数r记为r=abmodb,例如4=9bmod5,如图所示,若输入a=209,b=77,则循环体“r←abmodb”被执行了4次.
我们把b除a的余数r记为r=abmodb,例如4=9bmod5,如图所示,若输入a=209,b=77,则循环体“r←abmodb”被执行了4次.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com