
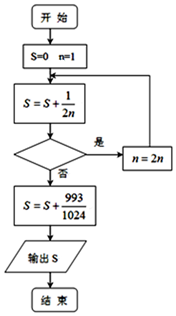
| A. | n<10 | B. | n≤10 | C. | n≤1024 | D. | n<1024 |
分析 分析程序框图的运行过程,得出程序输出的算式S的表达式,列出方程求出n的值,即可得出结论.
解答 解:本程序的功能是计算S=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{{2}^{k}}$=$\frac{\frac{1}{2}(1-\frac{1}{{2}^{k}})}{1-\frac{1}{2}}$=1-$\frac{1}{{2}^{k}}$,
∵S+$\frac{993}{1024}$=$\frac{2016}{2014}$,
∴S=$\frac{2013}{2014}$,
∴1-$\frac{1}{{2}^{k}}$=$\frac{2013}{2014}$,
∴$\frac{1}{{2}^{k}}$=$\frac{1}{{2}^{10}}$,
∴k=10,即运行了10次,
故可判断框内可填入的条件n≤210=1024,
故选:C
点评 本题主要考查程序框图的识别和判断,等比数列的求和公式,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | a<-2,或a>7 | B. | -2<a<7 | C. | -7<a<2 | D. | a=-2,或a=7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+1 | B. | x-1 | C. | x-2 | D. | x-$\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
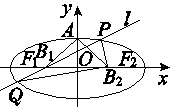 如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1,F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为4的直角三角形.过B1作l交椭圆于P、Q两点,使PB2垂直QB2,求直线l的方程x+2y+2=0和x-2y+2=0.
如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1,F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为4的直角三角形.过B1作l交椭圆于P、Q两点,使PB2垂直QB2,求直线l的方程x+2y+2=0和x-2y+2=0.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 幂函数 | B. | 对数函数 | C. | 指数函数 | D. | 一次函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | $4\sqrt{5}$ | C. | $6\sqrt{2}$ | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
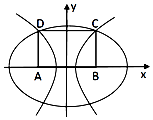 在平面直角坐标系xOy中,矩形ABCD的一边AB在x轴上,另一边CD在x轴上方,且AB=8,BC=6,其中A(-4,0)、B(4,0).
在平面直角坐标系xOy中,矩形ABCD的一边AB在x轴上,另一边CD在x轴上方,且AB=8,BC=6,其中A(-4,0)、B(4,0).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com