
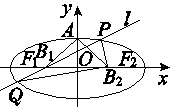
 如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1,F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为4的直角三角形.过B1作l交椭圆于P、Q两点,使PB2垂直QB2,求直线l的方程x+2y+2=0和x-2y+2=0.
如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1,F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为4的直角三角形.过B1作l交椭圆于P、Q两点,使PB2垂直QB2,求直线l的方程x+2y+2=0和x-2y+2=0. 分析 由题意设出椭圆的标准方程,结合已知列式求出椭圆方程,再设出直线l的方程x=my-2,联立直线方程和椭圆方程,化为关于y的一元二次方程,由根与系数的关系结合向量数量积为0列式求得m值,则直线方程可求.
解答 解:设所求椭圆的标准方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),右焦点为F2(c,0).
∵△AB1B2是直角三角形,又|AB1|=|AB2|,∴∠B1AB2为直角,
因此|OA|=|OB2|,得b=$\frac{c}{2}$.
结合c2=a2-b2,得4b2=a2-b2,故a2=5b2,c2=4b2,∴离心率e=$\frac{c}{a}$=$\frac{2}{5}$$\sqrt{5}$.
在Rt△AB1B2中,OA⊥B1B2,故${S}_{△A{B}_{1}{B}_{2}}$=$\frac{1}{2}$•|B1B2|•|OA|=|OB2|•|OA|=$\frac{c}{2}$•b=b2.
由题设条件△AB1B2的面积为4,得b2=4,从而a2=5b2=20.
因此所求椭圆的标准方程为:$\frac{{x}^{2}}{20}+\frac{{y}^{2}}{4}=1$.
则B1(-2,0),B2(2,0).
由题意知直线l的倾斜角不为0,故可设直线l的方程为:x=my-2.
代入椭圆方程得(m2+5)y2-4my-16=0.
设P(x1,y1),Q(x2,y2),则${y}_{1}{y}_{2}=-\frac{16}{{m}^{2}+5}$.
又$\overrightarrow{{B}_{2}Q}=({x}_{2}-2,{y}_{2})$,
∴由PB2⊥QB2,得$\overrightarrow{{B}_{2}P}•\overrightarrow{Q{B}_{2}}=0$,
即16m2-64=0,解得m=±2.
∴满足条件的直线有两条,其方程分别为x+2y+2=0和x-2y+2=0,
故答案为:x+2y+2=0和x-2y+2=0.
点评 本题考查椭圆的简单性质,考查了直线与椭圆位置关系的应用,体现了“设而不求”的解题思想方法和数学转化思想方法,是中档题.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | 命题p:“?x0∈R,$x_0^2-2{x_0}+1<0$”,则命题?p:?x∈R,x2-2x+1>0 | |
| B. | “lna>lnb”是“2a>2b”的充要条件 | |
| C. | 命题“若x2=2,则$x=\sqrt{2}$或$x=-\sqrt{2}$”的逆否命题是“若$x≠\sqrt{2}$或$x≠-\sqrt{2}$,则x2≠2” | |
| D. | 命题p:?x0∈R,1-x0<lnx0;命题q:对?x∈R,总有2x>0;则p∧q是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $3\sqrt{3}$ | B. | 2$\sqrt{5}$ | C. | $4\sqrt{5}$ | D. | $-4\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
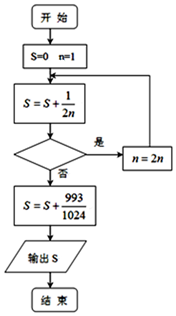
| A. | n<10 | B. | n≤10 | C. | n≤1024 | D. | n<1024 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=(x+1)2,x∈(0,+∞) | B. | y=log${\;}_{\frac{1}{2}}$x,x∈(1,+∞) | ||
| C. | y=2x-1 | D. | y=$\sqrt{2x-1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com