
分析 证法一:设0<x1<x2,作差判断f(x1)与f(x2)的大小,根据函数单调性的定义,可得f(x)=-x2+3在(0,+∞)上是减函数.
证法二:求导,根据当x∈(0,+∞)时,f′(x)<0恒成立,可得:f(x)=-x2+3在(0,+∞)上是增函数
解答 证法一:设0<x1<x2…(2分)
则$f({x_1})-f({x_2})=-x_1^2+3-({-x_2^2+3})$…(4分)
=$x_2^2-x_1^2=({{x_2}+{x_1}})({{x_2}-{x_1}})$…(6分)
∵0<x1<x2,
∴x2+x1>0,x2-x1>0,
∴f(x1)-f(x2)>0
∴f(x1)>f(x2),
∴f(x)=-x2+3在(0,+∞)上是增函数…(10分)
证法二:∵f(x)=-x2+3,
∴f′(x)=-2x,…(4分)
当x∈(0,+∞)时,
f′(x)<0恒成立,…(8分)
∴f(x)=-x2+3在(0,+∞)上是增函数…(10分)
点评 本题考查的知识点是利用导数研究函数的单调性,难度中档.


科目:高中数学 来源: 题型:选择题
| A. | x-2y-7=0 | B. | 2x+y+1=0 | C. | x-2y+7=0 | D. | 2x+y-1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<-2,或a>7 | B. | -2<a<7 | C. | -7<a<2 | D. | a=-2,或a=7 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 设U=R,集合A={x|-2<x<1},B={x|-1<x≤4},则如图中阴影部分表示的集合为{x|x≤-2,或-1<x<1,或x>4}.
设U=R,集合A={x|-2<x<1},B={x|-1<x≤4},则如图中阴影部分表示的集合为{x|x≤-2,或-1<x<1,或x>4}.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,+∞] | B. | (-1,0] | C. | (-1,+∞) | D. | (-1,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+1 | B. | x-1 | C. | x-2 | D. | x-$\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
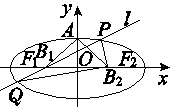 如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1,F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为4的直角三角形.过B1作l交椭圆于P、Q两点,使PB2垂直QB2,求直线l的方程x+2y+2=0和x-2y+2=0.
如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1,F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为4的直角三角形.过B1作l交椭圆于P、Q两点,使PB2垂直QB2,求直线l的方程x+2y+2=0和x-2y+2=0.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com