
分析 分离变量,利用函数的单调性求解即可.
解答 解:不等式($\frac{1}{2}$)x+($\frac{1}{3}$)x-m≥0,可得不等式($\frac{1}{2}$)x+($\frac{1}{3}$)x≥m,在x∈(-∞,1]时恒成立,
因为函数y=($\frac{1}{2}$)x+($\frac{1}{3}$)x,在x∈(-∞,1]是减函数,函数的最小值为:f(1)=$\frac{1}{2}+\frac{1}{3}$=$\frac{5}{6}$,
则实数m的取值范围是:(-∞,$\frac{5}{6}$].
故答案为:(-∞,$\frac{5}{6}$].
点评 本题考查函数恒成立,函数的单调性的应用,考查转化思想以及计算能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
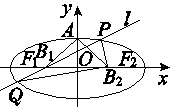 如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1,F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为4的直角三角形.过B1作l交椭圆于P、Q两点,使PB2垂直QB2,求直线l的方程x+2y+2=0和x-2y+2=0.
如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1,F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为4的直角三角形.过B1作l交椭圆于P、Q两点,使PB2垂直QB2,求直线l的方程x+2y+2=0和x-2y+2=0.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (k+1)3 | B. | (k+1)3+k3 | C. | (k-1)3+k3 | D. | (2k+1)(k+1)3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 17 | B. | 21 | C. | 23 | D. | 29 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com