
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 逐项判断即可.①由ac=bc不能推出a=b;②由5是有理数易判断;③根据不等式的性质可得;④根据充分必要条件的定义易得.
解答 解:①由“a=b“可得ac=bc,但当ac=bc时,不能得到a=b,故“a=b”是“ac=bc”的充分不必要条件,故①错误;
②因为5是有理数,所以当a+5是无理数时,a必为无理数,反之也成立,故②正确;
③取a=1,b=-2,此时a2<b2,故③错误;
④当a<4时,不能推出a<3;当a<3时,有a<4成立,故“a<4”是“a<3”的必要不充分条件,故④正确.
综上可得正确的命题有2个.
故选:B.
点评 本题考查充分必要条件的判断,掌握充分必要条件的定义是关键.属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
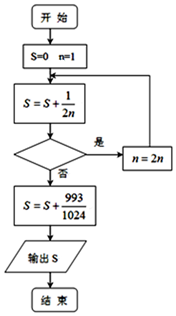
| A. | n<10 | B. | n≤10 | C. | n≤1024 | D. | n<1024 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 我们把b除a的余数r记为r=abmodb,例如4=9bmod5,如图所示,若输入a=209,b=77,则循环体“r←abmodb”被执行了4次.
我们把b除a的余数r记为r=abmodb,例如4=9bmod5,如图所示,若输入a=209,b=77,则循环体“r←abmodb”被执行了4次.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com