
| A. | 命题p:“?x0∈R,$x_0^2-2{x_0}+1<0$”,则命题?p:?x∈R,x2-2x+1>0 | |
| B. | “lna>lnb”是“2a>2b”的充要条件 | |
| C. | 命题“若x2=2,则$x=\sqrt{2}$或$x=-\sqrt{2}$”的逆否命题是“若$x≠\sqrt{2}$或$x≠-\sqrt{2}$,则x2≠2” | |
| D. | 命题p:?x0∈R,1-x0<lnx0;命题q:对?x∈R,总有2x>0;则p∧q是真命题 |
分析 对于A,特称命题的否定,先换量词,再否定结论;对于B,利用自然对数的定义及性质判定;对于C,“且”的否定时“或”;对于D,当命题p和q都真,p∧q是真.
解答 解:对于A,特称命题的否定,先换量词,再否定结论,小于的否定是大于或等于,故A错;
对于B利用自然对数的定义及性质要求a>b>0,可是由2a>2b;只能得到a>b,不一定大于0,故B错;
对于C,“且”的否定时“或”,故C错;
对于D,命题p中,如x0=2等成立,命题q 显然成立,当命题p和q都真,p∧q是真,故D为真命题.
故选:D.
点评 本题考查命题的真假判断与应用,着重考查四种命题之间的关系及真假判断,含有逻辑联结词的命题的否定与否命题,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-2y-7=0 | B. | 2x+y+1=0 | C. | x-2y+7=0 | D. | 2x+y-1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 336 | B. | 337 | C. | 1676 | D. | 2017 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{a}$<$\frac{1}{b}$ | B. | a3>b3 | C. | $\frac{1}{a}$>$\frac{1}{b}$ | D. | a2>b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<-2,或a>7 | B. | -2<a<7 | C. | -7<a<2 | D. | a=-2,或a=7 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 设U=R,集合A={x|-2<x<1},B={x|-1<x≤4},则如图中阴影部分表示的集合为{x|x≤-2,或-1<x<1,或x>4}.
设U=R,集合A={x|-2<x<1},B={x|-1<x≤4},则如图中阴影部分表示的集合为{x|x≤-2,或-1<x<1,或x>4}.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
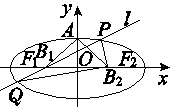 如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1,F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为4的直角三角形.过B1作l交椭圆于P、Q两点,使PB2垂直QB2,求直线l的方程x+2y+2=0和x-2y+2=0.
如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1,F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为4的直角三角形.过B1作l交椭圆于P、Q两点,使PB2垂直QB2,求直线l的方程x+2y+2=0和x-2y+2=0.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com