
| A. | 幂函数 | B. | 对数函数 | C. | 指数函数 | D. | 一次函数 |
分析 利用幂函数、对数函数、指数函数、一次函数的性质求解.
解答 解:在A中,幂函数不满足性质“对任意的x>0,y>0,函数f(x)满足“f(x+y)=f(x)•f(y)”,故A错误;
在B中,对数函数不满足性质“对任意的x>0,y>0,函数f(x)满足“f(x+y)=f(x)•f(y)”,故B错误;
在C中,指数函数满足性质“对任意的x>0,y>0,函数f(x)满足“f(x+y)=f(x)•f(y)”,故C正确;
在D中,一次函数不满足性质“对任意的x>0,y>0,函数f(x)满足“f(x+y)=f(x)•f(y)”,故D错误.
故选:C.
点评 本题考查幂函数、对数函数、指数函数、一次函数的性质的应用,是基础题,解题要要认真审题,熟练掌握幂函数、对数函数、指数函数、一次函数的性质.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0<a≤$\frac{1}{3}$ | B. | a≤$\frac{1}{3}$ | C. | $\frac{1}{3}$≤a<1 | D. | a≥3或0<a<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $3\sqrt{3}$ | B. | 2$\sqrt{5}$ | C. | $4\sqrt{5}$ | D. | $-4\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 6 | C. | 9$\sqrt{3}$ | D. | 6$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
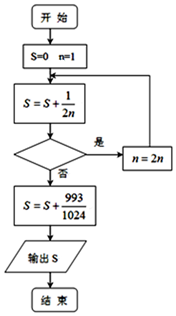
| A. | n<10 | B. | n≤10 | C. | n≤1024 | D. | n<1024 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | $-\frac{1}{5}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com