
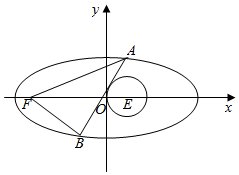
 过圆E:(x-1)2+y2=1上的点M(${\frac{3}{2}$,$\frac{{\sqrt{3}}}{2}}$)作圆的切线l,切线l与坐标轴的两个交点分别为椭圆C的两个顶点.
过圆E:(x-1)2+y2=1上的点M(${\frac{3}{2}$,$\frac{{\sqrt{3}}}{2}}$)作圆的切线l,切线l与坐标轴的两个交点分别为椭圆C的两个顶点.分析 (1)利用直线与圆相切的性质、点到直线的距离公式即可得出.
(2)当直线AB的斜率不存在时,有两种情况:①切点为原点,切线为y轴,此时|AF|+|BF|=6;
②切点为圆E与x轴的另一交点N(2,0),此时直接得出;当斜率存在时,设方程为y=kx+m,因为与圆E相切,得$\frac{{|{k+m}|}}{{\sqrt{1+{k^2}}}}=1,2km+{m^2}=1$,显然m≠0,$k=\frac{{1-{m^2}}}{2m}$,与椭圆的方程联立转化为根与系数的关系,再利用导数研究函数的单调性即可得出.
解答 解:(1)设过点M的圆E的切线方程为$y-\frac{{\sqrt{3}}}{2}=k({x-\frac{3}{2}})$,则圆心(1,0)到这条直线的距离是$d=\frac{{|{-\frac{1}{2}k+\frac{{\sqrt{3}}}{2}}|}}{{\sqrt{1+{k^2}}}}=1$,得$k=-\frac{{\sqrt{3}}}{3}$,
∴切线l方程为$y-\frac{{\sqrt{3}}}{2}=-\frac{{\sqrt{3}}}{3}({x-\frac{3}{2}})$,当x=0时,$y=\sqrt{3}$,当y=0时,x=3.
由题意得,椭圆E的方程为:$\frac{x^2}{9}+\frac{y^2}{3}=1$.
(2)当直线AB的斜率不存在时,有两种情况:①切点为原点,切线为y轴,此时|AF|+|BF|=6;
②切点为圆E与x轴的另一交点N(2,0),此时$A({2,\frac{{\sqrt{15}}}{3}}),B({2,-\frac{{\sqrt{15}}}{3}}),|{AF}|+|{BF}|=2|{AF}|=2\sqrt{{{({2+\sqrt{6}})}^2}+{{({\frac{{\sqrt{15}}}{3}})}^2}}=2\sqrt{\frac{{35+12\sqrt{6}}}{3}}=\frac{2}{3}\sqrt{105+36\sqrt{6}}>6$.
当斜率存在时,设方程为y=kx+m,因为与圆E相切,得$\frac{{|{k+m}|}}{{\sqrt{1+{k^2}}}}=1,2km+{m^2}=1$,显然m≠0,∴$k=\frac{{1-{m^2}}}{2m}$,
把y=kx+m代入$\frac{x^2}{9}+\frac{y^2}{3}=1$得:(1+3k2)x2+6kmx+3m2-9=0.
设A(x1,y1),B(x2,y2),则${x_1}+{x_2}=\frac{-6km}{{1+3{k^2}}}$,
又知椭圆C的离心率$e=\frac{{\sqrt{6}}}{3}$,∴$|{AF}|+|{BF}|=\frac{{\sqrt{6}}}{3}({{x_1}+{x_2}})+6=\frac{{\sqrt{6}}}{3}×\frac{-6km}{{1+3{k^2}}}+6$=$-4\sqrt{6}×\frac{{-{m^2}+{m^2}}}{{3{m^4}-2{m^2}+3}}+6$,
令$t={m^2}({t>0}),g(t)=\frac{{-{t^2}+t}}{{3{t^2}-2t+3}},g'(x)=\frac{{-{t^2}-6t+3}}{{{{({3{t^2}-2t+3})}^2}}}$,令t2+6t-3=0,解得$t=-3+2\sqrt{3}$或$t=-3-2\sqrt{3}$(舍去).
当$t=-3+2\sqrt{3}$时,g(t)取得最大值,此时|AF|+|BF|取得最小值为$6+\frac{{\sqrt{6}-3\sqrt{2}}}{2}<6$,故|AF|+|BF|取得最小值为$6+\frac{{\sqrt{6}-3\sqrt{2}}}{2}$.
点评 本题考查了椭圆的标准方程、直线与圆相切的性质、一元二次方程的根与系数的关系、点到直线的距离公式,考查了分类讨论方法、推理能力与计算能力,属于难题.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:选择题
| A. | k+1 | B. | 2k+1 | C. | k2+1 | D. | (k+1)2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | (-∞,1] | C. | [0,3] | D. | (-∞,1]∪[3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
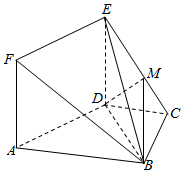 如图,边长为$\sqrt{2}$的正方形ADEF与梯形ABCD所在的平面互相垂直,其中AB∥CD,AB⊥BC,CD=BC=$\frac{1}{2}$AB=1,点M在线段EC上.
如图,边长为$\sqrt{2}$的正方形ADEF与梯形ABCD所在的平面互相垂直,其中AB∥CD,AB⊥BC,CD=BC=$\frac{1}{2}$AB=1,点M在线段EC上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com