
分析 根据题意可得可得|2x+1|>|$\frac{x}{2}$+1|①,且|2x+1|≤1 ②.分别求得①、②的解集,再取交集,即为所求.
解答 解:根据函数f(x)为定义在[-1,1]上的偶函数,且在[0,1]上为单调递增函数,
则由f(2x+1)>f(${\frac{x}{2}$+1),可得|2x+1|>|$\frac{x}{2}$+1|①,且|2x+1|≤1 ②.
把①平方可得x($\frac{5}{4}$x+1)>0,∴x<-$\frac{4}{5}$,或x>0.
由②可得-1≤2x+1≤1,解得-1≤x≤0.
综合可得,-1≤x<-$\frac{4}{5}$,
故答案为:[-1,-$\frac{4}{5}$).
点评 本题主要考查函数的单调性和奇偶性的综合,绝对值不等式的解集,属于基础题.


科目:高中数学 来源: 题型:选择题
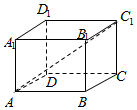 长方体ABCD-A1B1C1D1中,已知A1A=$\sqrt{2}$,AD=1,AB=1,则对角线AC1与平面ABCD所成角为( )
长方体ABCD-A1B1C1D1中,已知A1A=$\sqrt{2}$,AD=1,AB=1,则对角线AC1与平面ABCD所成角为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 本数 人数 性别 | 0 | 1 | 2 | 3 | 4 | 5 |
| 男生 | 0 | 1 | 4 | 3 | 2 | 2 |
| 女生 | 0 | 0 | 1 | 3 | 3 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
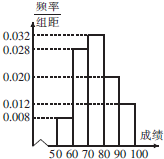 博鳌亚洲论坛2015年会员大会于3月27日在海南博鳌举办,大会组织者对招募的100名服务志愿者培训后,组织一次APEC知识竞赛,将所得成绩制成如右频率分布直方图(假定每个分数段内的成绩均匀分布),组织者计划对成绩前20名的参赛者进行奖励.
博鳌亚洲论坛2015年会员大会于3月27日在海南博鳌举办,大会组织者对招募的100名服务志愿者培训后,组织一次APEC知识竞赛,将所得成绩制成如右频率分布直方图(假定每个分数段内的成绩均匀分布),组织者计划对成绩前20名的参赛者进行奖励.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
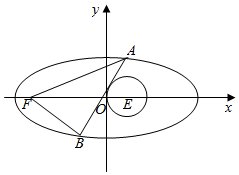 过圆E:(x-1)2+y2=1上的点M(${\frac{3}{2}$,$\frac{{\sqrt{3}}}{2}}$)作圆的切线l,切线l与坐标轴的两个交点分别为椭圆C的两个顶点.
过圆E:(x-1)2+y2=1上的点M(${\frac{3}{2}$,$\frac{{\sqrt{3}}}{2}}$)作圆的切线l,切线l与坐标轴的两个交点分别为椭圆C的两个顶点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3π | B. | $\frac{16}{3}$π | C. | 6π | D. | $\frac{20}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 既是奇函数,又是偶函数 | D. | 非奇非偶函数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com