
【题目】某工厂有甲,乙两个车间生产同一种产品,,甲车间有工人![]() 人,乙车间有工人
人,乙车间有工人![]() 人,为比较两个车间工人的生产效率,采用分层抽样的方法抽取工人,甲车间抽取的工人记作第一组,乙车间抽取的工人记作第二组,并对他们中每位工人生产完成的一件产品的事件(单位:
人,为比较两个车间工人的生产效率,采用分层抽样的方法抽取工人,甲车间抽取的工人记作第一组,乙车间抽取的工人记作第二组,并对他们中每位工人生产完成的一件产品的事件(单位:![]() )进行统计,按照
)进行统计,按照![]() 进行分组,得到下列统计图.
进行分组,得到下列统计图.

![]() 分别估算两个车间工人中,生产一件产品时间少于
分别估算两个车间工人中,生产一件产品时间少于![]() 的人数
的人数
![]() 分别估计两个车间工人生产一件产品时间的平均值,并推测车哪个车间工人的生产效率更高?
分别估计两个车间工人生产一件产品时间的平均值,并推测车哪个车间工人的生产效率更高?
![]() 从第一组生产时间少于
从第一组生产时间少于![]() 的工人中随机抽取
的工人中随机抽取![]() 人,记抽取的生产时间少于
人,记抽取的生产时间少于![]() 的工人人数为随机变量
的工人人数为随机变量![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
【答案】![]() 60,300;
60,300;![]() 乙车间工人生产效率更高;
乙车间工人生产效率更高;![]() 见解析.
见解析.
【解析】
(Ⅰ)由图表分别计算出两个车间生产一件产品时间少于![]() 的人数;
的人数;
(Ⅱ)分别计算两个车间工人生产一件产品时间的平均值,从而得到结果;
(Ⅲ)![]() 可取值为
可取值为![]() .计算出相应的概率值,得到分布列与期望.
.计算出相应的概率值,得到分布列与期望.
(Ⅰ)由题意得,第一组工人![]() 人,其中在
人,其中在![]() 内(不含
内(不含![]() )生产完成一件产品的有
)生产完成一件产品的有![]() 人
人
![]() 甲车间工人中生产一件产品时间少于
甲车间工人中生产一件产品时间少于![]() 的人数为
的人数为![]() (人)
(人)
第二组工人![]() 人. 其中在
人. 其中在![]() 内(不含
内(不含![]() )生产完成一件产品的有
)生产完成一件产品的有![]() 人
人
![]() 乙车间工人中生产一件产品时间少于
乙车间工人中生产一件产品时间少于![]() 的人数为
的人数为![]() (人)
(人)
(Ⅱ)第一组平均时间为![]() .
.
第二组平均时间为![]() .
.
![]() ,
,![]() 乙车间工人生产效率更高;
乙车间工人生产效率更高;
(Ⅲ)由题意得,第一组生产时间少于![]() 的工人有
的工人有![]() 人,从中抽取
人,从中抽取![]() 人,其中生产时间少于
人,其中生产时间少于![]() 的有
的有![]() 人.
人.
![]() 可取值为
可取值为![]() .
.
![]() .
.
![]() ,
,
![]() ,
,
![]() 的分布列为:
的分布列为:

数学期望![]() .
.


科目:高中数学 来源: 题型:
【题目】某乐园按时段收费,收费标准为:每玩一次不超过![]() 小时收费10元,超过
小时收费10元,超过![]() 小时的部分每小时收费
小时的部分每小时收费![]() 元(不足
元(不足![]() 小时的部分按
小时的部分按![]() 小时计算).现有甲、乙二人参与但都不超过
小时计算).现有甲、乙二人参与但都不超过![]() 小时,甲、乙二人在每个时段离场是等可能的。为吸引顾客,每个顾客可以参加一次抽奖活动。
小时,甲、乙二人在每个时段离场是等可能的。为吸引顾客,每个顾客可以参加一次抽奖活动。
(1) 用![]() 表示甲乙玩都不超过
表示甲乙玩都不超过![]() 小时的付费情况,求甲、乙二人付费之和为44元的概率;
小时的付费情况,求甲、乙二人付费之和为44元的概率;
(2)抽奖活动的规则是:顾客通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数![]() ,并按如右所示的程序框图执行.若电脑显示“中奖”,则该顾客中奖;若电脑显示“谢谢”,则不中奖,求顾客中奖的概率.
,并按如右所示的程序框图执行.若电脑显示“中奖”,则该顾客中奖;若电脑显示“谢谢”,则不中奖,求顾客中奖的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】槟榔原产于马来西亚,中国主要分布在云南、海南及台湾等热带地区,在亚洲热带地区广泛栽培.槟榔是重要的中药材,在南方一些少数民族还有将果实作为一种咀嚼嗜好品,但其被世界卫生组织国际癌症研究机构列为致癌物清单Ⅰ类致癌物.云南某民族中学为了解![]() ,
,![]() 两个少数民族班学生咀嚼槟榔的情况,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周咀嚼槟榔的颗数作为样本绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
两个少数民族班学生咀嚼槟榔的情况,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周咀嚼槟榔的颗数作为样本绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
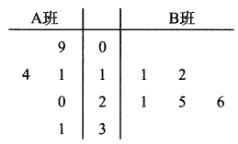
(1)你能否估计哪个班级学生平均每周咀嚼槟榔的颗数较多?
(2)从![]() 班的样本数据中随机抽取一个不超过19的数据记为
班的样本数据中随机抽取一个不超过19的数据记为![]() ,从
,从![]() 班的样本数据中随机抽取一个不超过21的数据记为
班的样本数据中随机抽取一个不超过21的数据记为![]() ,求
,求![]() 的概率;
的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2﹣2x﹣4y+m=0.
(1)若圆C与直线l:x+2y﹣4=0相交于M、N两点,且|MN|![]() ,求m的值;
,求m的值;
(2)在(1)成立的条件下,过点P(2,1)引圆的切线,求切线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古达数学名著《九章算术-商功》中阐述:“斜解立方,得两堑堵,斜解堑堵,其一为阳马,一为鳖觸,阳马居二,鳖属居一.不易之率也。合两鳖觸三而一,验之以基,其形露矣,”若称为“阳马”的某几何体的三视图如图所示 图中网格纸上小正方形的边长为![]() . 则对该儿何体描述:
. 则对该儿何体描述:
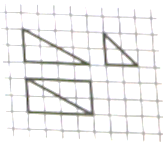
①四个侧面首饰直角三角形
②最长的侧棱长为![]()
③四个侧面中有三个侧面是全等的直角三角形
④外接球的表面积为![]()
其中正确的个数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据指令![]() (
(![]() ,
,![]() ),机器人在平面上能完成下列动作,先原地旋转弧度
),机器人在平面上能完成下列动作,先原地旋转弧度![]() (
(![]() 为正时,按逆时针方向旋转
为正时,按逆时针方向旋转![]() ,
,![]() 为负时,按顺时针方向旋转
为负时,按顺时针方向旋转![]() ),再朝其面对的方向沿直线行走距离r;
),再朝其面对的方向沿直线行走距离r;
(1)现机器人在平面直角坐标系的坐标原点,且面对x轴正方向,试给机器人下一个指令,使其移动到点![]() ;
;
(2)机器人在完成该指令后,发现在点![]() 处有一小球,正向坐标原点作匀速直线滚动,已知小球滚动的速度为机器人直线行走速度的2倍,若忽略机器人原地旋转所需的时间,问机器人最快可在何处截住小球?并给出机器人截住小球所需的指令?(结果用反三角函数表示)
处有一小球,正向坐标原点作匀速直线滚动,已知小球滚动的速度为机器人直线行走速度的2倍,若忽略机器人原地旋转所需的时间,问机器人最快可在何处截住小球?并给出机器人截住小球所需的指令?(结果用反三角函数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四面体A-BCD中,有两条棱的长为![]()
![]() ,其余棱的长度都为1;
,其余棱的长度都为1;
(1)若![]() ,且
,且![]() ,求二面角A-BC-D的余弦值;
,求二面角A-BC-D的余弦值;
(2)求a的取值范围,使得这样的四面体是存在的;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的渐近线方程为
的渐近线方程为![]() ,一个焦点为
,一个焦点为![]() .
.
(1)求双曲线![]() 的方程;
的方程;
(2)过双曲线![]() 上的任意一点
上的任意一点![]() ,分别作这两条渐近线的平行线与这两条渐近线得到四边形
,分别作这两条渐近线的平行线与这两条渐近线得到四边形![]() ,证明四边形
,证明四边形![]() 的面积是一个定值;
的面积是一个定值;
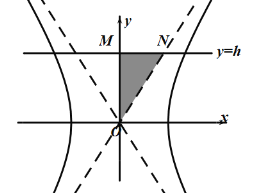
(3)设直线![]() 与
与![]()
![]() 在第一象限内与渐近线
在第一象限内与渐近线![]() 所围成的三角形
所围成的三角形![]() 绕着
绕着![]() 轴旋转一周所得几何体的体积.
轴旋转一周所得几何体的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com