
【题目】我国古达数学名著《九章算术-商功》中阐述:“斜解立方,得两堑堵,斜解堑堵,其一为阳马,一为鳖觸,阳马居二,鳖属居一.不易之率也。合两鳖觸三而一,验之以基,其形露矣,”若称为“阳马”的某几何体的三视图如图所示 图中网格纸上小正方形的边长为![]() . 则对该儿何体描述:
. 则对该儿何体描述:
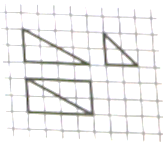
①四个侧面首饰直角三角形
②最长的侧棱长为![]()
③四个侧面中有三个侧面是全等的直角三角形
④外接球的表面积为![]()
其中正确的个数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的方程为
的方程为![]() ,
,![]() 是椭圆上的一点,且
是椭圆上的一点,且![]() 在第一象限内,过
在第一象限内,过![]() 且斜率等于-1的直线与椭圆
且斜率等于-1的直线与椭圆![]() 交于另一点
交于另一点![]() ,点
,点![]() 关于原点的对称点为
关于原点的对称点为![]() .
.
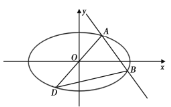
(1)证明:直线![]() 的斜率为定值;
的斜率为定值;
(2)求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“科技引领,布局未来”科技研发是企业发展的驱动力量。![]() 年,某企业连续
年,某企业连续![]() 年累计研发投入搭
年累计研发投入搭![]() 亿元,我们将研发投入与经营投入的比值记为研发投入占营收比,这
亿元,我们将研发投入与经营投入的比值记为研发投入占营收比,这![]() 年间的研发投入(单位:十亿元)用右图中的折现图表示,根据折线图和条形图,下列结论错误的使( )
年间的研发投入(单位:十亿元)用右图中的折现图表示,根据折线图和条形图,下列结论错误的使( )
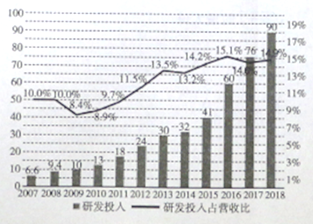
A. ![]() 年至
年至![]() 年研发投入占营收比增量相比
年研发投入占营收比增量相比![]() 年至
年至![]() 年增量大
年增量大
B. ![]() 年至
年至![]() 年研发投入增量相比
年研发投入增量相比![]() 年至
年至![]() 年增量小
年增量小
C. 该企业连续![]() 年研发投入逐年增加
年研发投入逐年增加
D. 该企业来连续![]() 年来研发投入占营收比逐年增加
年来研发投入占营收比逐年增加
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂有甲,乙两个车间生产同一种产品,,甲车间有工人![]() 人,乙车间有工人
人,乙车间有工人![]() 人,为比较两个车间工人的生产效率,采用分层抽样的方法抽取工人,甲车间抽取的工人记作第一组,乙车间抽取的工人记作第二组,并对他们中每位工人生产完成的一件产品的事件(单位:
人,为比较两个车间工人的生产效率,采用分层抽样的方法抽取工人,甲车间抽取的工人记作第一组,乙车间抽取的工人记作第二组,并对他们中每位工人生产完成的一件产品的事件(单位:![]() )进行统计,按照
)进行统计,按照![]() 进行分组,得到下列统计图.
进行分组,得到下列统计图.

![]() 分别估算两个车间工人中,生产一件产品时间少于
分别估算两个车间工人中,生产一件产品时间少于![]() 的人数
的人数
![]() 分别估计两个车间工人生产一件产品时间的平均值,并推测车哪个车间工人的生产效率更高?
分别估计两个车间工人生产一件产品时间的平均值,并推测车哪个车间工人的生产效率更高?
![]() 从第一组生产时间少于
从第一组生产时间少于![]() 的工人中随机抽取
的工人中随机抽取![]() 人,记抽取的生产时间少于
人,记抽取的生产时间少于![]() 的工人人数为随机变量
的工人人数为随机变量![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 在回归模型中,预报变量![]() 的值不能由解释变量
的值不能由解释变量![]() 唯一确定
唯一确定
B. 若变量![]() ,
,![]() 满足关系
满足关系![]() ,且变量
,且变量![]() 与
与![]() 正相关,则
正相关,则![]() 与
与![]() 也正相关
也正相关
C. 在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高
D. 以模型![]() 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设![]() ,将其变换后得到线性方程
,将其变换后得到线性方程![]() ,则
,则![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
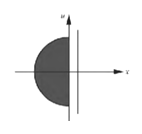
【题目】关于旋转体的体积,有如下的古尔丁(guldin)定理:“平面上一区域D绕区域外一直线(区域D的每个点在直线的同侧,含直线上)旋转一周所得的旋转体的体积,等于D的面积与D的几何中心(也称为重心)所经过的路程的乘积”.利用这一定理,可求得半圆盘 ,绕直线x
,绕直线x![]() 旋转一周所形成的空间图形的体积为_____.
旋转一周所形成的空间图形的体积为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com