【答案】
分析:(1)由b
2+c
2≥2bc,a>0,证得 a(b
2+c
2)≥2abc,同理可证 b(c
2+a
2)≥2abc,相乘即可得到要证的结论.
(2)直接法利用分析法进行证明.
解答:证明:(1)∵b
2+c
2≥2bc,a>0,∴a(b
2+c
2)≥2abc.
又∵c
2+a
2≥2ac,b>0,∴b(c
2+a
2)≥2abc.
∴a(b
2+c
2)+b(c
2+a
2)≥4abc.
(2)∵
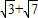
和

都是正数,
要证
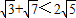
只需证
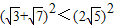
整理得:
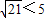
即证:21<25
∵21<25显然成立
∴原不等式成立
点评:本题(1)考查用综合法证明不等式,证明a(b
2+c
2)≥2abc,是解题的关键.(2)考查分析法证明不等式,重视分析法的证明步骤.

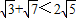 .
.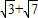 和
和 都是正数,
都是正数,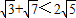
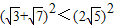
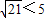


 名校课堂系列答案
名校课堂系列答案