
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(Ⅰ)若![]() ,求直线
,求直线![]() 被曲线
被曲线![]() 截得的线段的长度;
截得的线段的长度;
(Ⅱ)若![]() ,在曲线
,在曲线![]() 上求一点
上求一点![]() ,使得点
,使得点![]() 到直线
到直线![]() 的距离最小,并求出最小距离.
的距离最小,并求出最小距离.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
试题(Ⅰ)由题意,得曲线![]() 的普通方程和直线
的普通方程和直线![]() 的普通方程,联立方程组,解焦点,即可求解截曲线
的普通方程,联立方程组,解焦点,即可求解截曲线![]() 的线段长;
的线段长;
(Ⅱ)解法一:![]() 时,得直线
时,得直线![]() 的普通方程,由点到直线的距离公式,得到距离的表达式,转化为三角函数的性质,即可求解最小值.
的普通方程,由点到直线的距离公式,得到距离的表达式,转化为三角函数的性质,即可求解最小值.
试题解析:
(Ⅰ)曲线![]() 的普通方程为
的普通方程为![]() .
.
当![]() 时,直线
时,直线![]() 的普通方程为
的普通方程为![]() .
.
由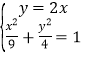 .解得
.解得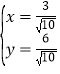 或
或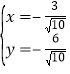 ,
,
直线![]() 被曲线
被曲线![]() 截得的线段的长度为
截得的线段的长度为![]() .
.
(Ⅱ)解法一:![]() 时,直线
时,直线![]() 的普通方程为
的普通方程为![]() .
.
由点到直线的距离公式,椭圆![]() 上的点
上的点![]() 到直线
到直线![]() :
:![]() 的距离为
的距离为
![]()
![]()
![]() ,
,
其中![]() 满足
满足![]() ,
,![]() .
.
由三角函数性质知,当![]() 时,
时,![]() 取最小值
取最小值![]() .
.
此时,![]() ,
,![]() .
.
因此,当点![]() 位于
位于![]() 时,点
时,点![]() 到
到![]() 的距离取最小值
的距离取最小值![]() .
.
解法二:当![]() 时,直线
时,直线![]() 的普通方程为
的普通方程为![]() .
.
设与![]() 平行,且与椭圆
平行,且与椭圆![]() 相切的直线
相切的直线![]() 的方程为
的方程为![]() .
.
由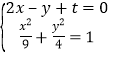 消去
消去![]() 并整理得
并整理得![]() .
.
由判别式![]() ,解得
,解得![]() .
.
所以,直线![]() 的方程为
的方程为![]() ,或
,或![]() .
.
要使两平行直线![]() 与
与![]() 间的距离最小,则直线
间的距离最小,则直线![]() 的方程为
的方程为![]() .
.
这时,![]() 与
与![]() 间的距离
间的距离![]()
![]() .
.
此时点![]() 的坐标为方程组
的坐标为方程组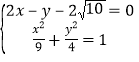 的解
的解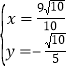 .
.
因此,当点![]() 位于
位于![]() 时,点
时,点![]() 到直线
到直线![]() 的距离取最小值
的距离取最小值![]() .
.


 小学教材全测系列答案
小学教材全测系列答案科目:高中数学 来源: 题型:
【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求回归直线方程![]() =bx+a;(其中
=bx+a;(其中 ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】5G网络是第五代移动通信网络,其峰值理论传输速度可达每8秒1GB,比4G网络的传输速度快数百倍.举例来说,一部1G的电影可在8秒之内下载完成.随着5G技术的诞生,用智能终端分享3D电影、游戏以及超高画质(UHD)节目的时代正向我们走来.某手机网络研发公司成立一个专业技术研发团队解决各种技术问题,其中有数学专业毕业,物理专业毕业,其它专业毕业的各类研发人员共计1200人.现在公司为提高研发水平,采用分层抽样抽取400人按分数对工作成绩进行考核,并整理得如上频率分布直方图(每组的频率视为概率).

(1)从总体的1200名学生中随机抽取1人,估计其分数小于50的概率;
(2)研发公司决定对达到某分数以上的研发人员进行奖励,要求奖励研发人员的人数达到30%,请你估计这个分数的值;
(3)已知样本中有三分之二的数学专业毕业的研发人员分数不低于70分,样本中不低于70分的数学专业毕业的研发人员人数与物理及其它专业毕业的研发人员的人数和相等,估计总体中数学专业毕业的研发人员的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,天津之眼,全称天津永乐桥摩天轮,是世界上唯一一个桥上瞰景摩天轮,是天津的地标之一 .永乐桥分上下两层,上层桥面预留了一个长方形开口,供摩天轮轮盘穿过,摩天轮的直径为110米,外挂装48个透明座舱,在电力的驱动下逆时针匀速旋转,转一圈大约需要30分钟.现将某一个透明座舱视为摩天轮上的一个点![]() ,当点
,当点![]() 到达最高点时,距离下层桥面的高度为113米,点
到达最高点时,距离下层桥面的高度为113米,点![]() 在最低点处开始计时.
在最低点处开始计时.

(1)试确定在时刻![]() (单位:分钟)时点
(单位:分钟)时点![]() 距离下层桥面的高度
距离下层桥面的高度![]() (单位:米);
(单位:米);
(2)若转动一周内某一个摩天轮透明座舱在上下两层桥面之间的运行时间大约为5分钟,问上层桥面距离下层桥面的高度约为多少米?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为某儿童游乐场一个小型摩天轮示意图,该摩天轮近似看作半径为![]() 的圆,圆上最低点A与地面距离为
的圆,圆上最低点A与地面距离为![]() ,摩天轮每60秒匀速转动一圈,摩天轮上某点B的起始位置在最低点A处.图中
,摩天轮每60秒匀速转动一圈,摩天轮上某点B的起始位置在最低点A处.图中![]() 与地面垂直,以
与地面垂直,以![]() 为始边,逆时针转动
为始边,逆时针转动![]() 角到
角到![]() ,设B点与地面间的距离为
,设B点与地面间的距离为![]() .
.
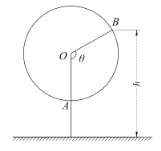
(1)求h与![]() 间关系的函数解析式;
间关系的函数解析式;
(2)设从![]() 开始转动,经过t秒后到达
开始转动,经过t秒后到达![]() ,求h与t之间的函数关系式;
,求h与t之间的函数关系式;
(3)如果离地面高度不低于![]() 才能获得最佳观景效果,在摩天轮转动的一圈内,有多长时间B点在最佳观景效果高度?
才能获得最佳观景效果,在摩天轮转动的一圈内,有多长时间B点在最佳观景效果高度?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司的电子新产品未上市时,原定每件售价100元,经过市场调研发现,该电子新产品市场潜力很大,该公司决定从第一周开始销售时,该电子产品每件售价比原定售价每周涨价4元,5周后开始保持120元的价格平稳销售,10周后由于市场竞争日益激烈,每周降价2元,直到15周结束,该产品不再销售.
(Ⅰ)求售价![]() (单位:元)与周次
(单位:元)与周次![]() (
(![]() )之间的函数关系式;
)之间的函数关系式;
(Ⅱ)若此电子产品的单件成本![]() (单位:元)与周次
(单位:元)与周次![]() 之间的关系式为
之间的关系式为![]() ,
,![]() ,
,![]() ,试问:此电子产品第几周的单件销售利润(销售利润
,试问:此电子产品第几周的单件销售利润(销售利润![]() 售价
售价![]() 成本)最大?
成本)最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为1的正方体![]() 中,点P在线段
中,点P在线段![]() 上运动,给出以下四个命题:
上运动,给出以下四个命题:

①异面直线![]() 与
与![]() 所成的角为定值;
所成的角为定值;
②二面角![]() 的大小为定值;
的大小为定值;
③三棱锥![]() 的体积为定值;
的体积为定值;
其中真命题的个数为( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面四边形![]() 中,
中, ![]() ,
, ![]() 为等边三角形,现将
为等边三角形,现将![]() 沿
沿![]() 翻折得到四面体
翻折得到四面体![]() ,点
,点![]() 分别为
分别为![]() 的中点.
的中点.


(Ⅰ)求证:四边形![]() 为矩形;
为矩形;
(Ⅱ)当平面![]() 平面
平面![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交通安全法有规定:机动车行经人行横道时,应当减速行驶;遇行人正在通过人行横道,应当停车让行.机动车行经没有交通信号的道路时,遇行人横过马路,应当避让.我们将符合这条规定的称为“礼让斑马线”,不符合这条规定的称为“不礼让斑马线”.下表是六安市某十字路口监控设备所抓拍的5个月内驾驶员“不礼让斑马线”行为的统计数据:
月份 | 1 | 2 | 3 | 4 | 5 |
“不礼让斑马线”的驾驶员人数 | 120 | 105 | 100 | 85 | 90 |
(1)根据表中所给的5个月的数据,可用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)求“不礼让斑马线”的驾驶员人数![]() 关于月份
关于月份![]() 之间的线性回归方程;
之间的线性回归方程;
(3)若从4,5月份“不礼让斑马线”的驾驶员中分别选取4人和2人,再从所选取的6人中任意抽取2人进行交规调查,求抽取的2人分别来自两个月份的概率;
参考公式:线性回归方程![]() ,其中
,其中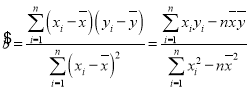 ,
,![]() ,
, .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com