
【题目】已知椭圆![]() :
:![]()
![]() 的一个焦点与抛物线
的一个焦点与抛物线![]() 的焦点重合,点
的焦点重合,点![]() 在
在![]() 上
上
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)直线![]() 不过原点O且不平行于坐标轴,
不过原点O且不平行于坐标轴,![]() 与
与![]() 有两个交点
有两个交点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,证明:
,证明:![]() 的斜率与直线
的斜率与直线![]() 的斜率的乘积为定值.
的斜率的乘积为定值.
【答案】(Ⅰ)![]() (Ⅱ)详见解析
(Ⅱ)详见解析
【解析】
试题分析:(Ⅰ)求得抛物线的焦点,可得c=2,再由点满足椭圆方程,结合a,b,c的关系,解方程可得椭圆的方程;(Ⅱ)设直线l的方程为y=kx+b(k,b≠0),A![]() ,B
,B![]() ,代入椭圆方程,运用韦达定理和中点坐标公式可得M的坐标,可得直线OM的斜率,进而得到证明
,代入椭圆方程,运用韦达定理和中点坐标公式可得M的坐标,可得直线OM的斜率,进而得到证明
试题解析:(Ⅰ)抛物线![]() 的焦点为(2,0),由题意可得c=2,即
的焦点为(2,0),由题意可得c=2,即![]() ,
,
又点![]() 在
在![]() 上,可得
上,可得![]() 解得
解得![]()
即有椭圆C:![]()
![]() …………………………5分
…………………………5分
(Ⅱ)证明:设直线![]() 的方程为
的方程为![]() (
(![]() ≠0),
≠0),![]() ,
,![]() ,…………6分
,…………6分
将直线![]() 代入椭圆方程
代入椭圆方程![]() ,可得
,可得
![]() ,
,![]() …………………………8分
…………………………8分
即有AB的中点M的横坐标为![]() ,纵坐标为
,纵坐标为![]() …………10分
…………10分
直线OM的斜率为![]()
![]() 即有
即有![]()
故OM的斜率与直线l的斜率的乘积为定值.…………………………12分


科目:高中数学 来源: 题型:
【题目】已知直线l与圆C:x2+y2+2x﹣4y+a=0相交于A,B两点,弦AB的中点为M(0,1).
(1)若圆C的半径为![]() ,求实数a的值;
,求实数a的值;
(2)若弦AB的长为6,求实数a的值;
(3)当a=1时,圆O:x2+y2=2与圆C交于M,N两点,求弦MN的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在(﹣∞,+∞)上的偶函数,且在(﹣∞,0]上是增函数,设a=f(log47),b=f(log ![]() 3),c=f(21.6),则a,b,c的大小关系是( )
3),c=f(21.6),则a,b,c的大小关系是( )
A.c<a<b
B.c<b<a
C.b<c<a
D.a<b<c
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线![]() 的顶点为坐标原点O,焦点F在
的顶点为坐标原点O,焦点F在![]() 轴正半轴上,准线
轴正半轴上,准线![]() 与圆
与圆![]() 相切.
相切.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)已知直线![]() 和抛物线
和抛物线![]() 交于点
交于点![]() ,命题
,命题![]() :“若直线
:“若直线![]() 过定点(0,1),则
过定点(0,1),则 ![]() ”,
”,
请判断命题![]() 的真假,并证明.
的真假,并证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,点
,点![]() 是椭圆上任意一点,
是椭圆上任意一点, ![]() 的周长为
的周长为![]() .
.
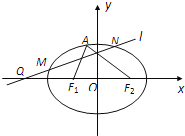
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() (-4,0)任作一动直线
(-4,0)任作一动直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,记
两点,记![]() ,若在线段
,若在线段![]() 上取一点
上取一点![]() ,使得
,使得![]() ,则当直线
,则当直线![]() 转动时,点
转动时,点![]() 在某一定直线上运动,求该定直线的方程.
在某一定直线上运动,求该定直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中心在原点,焦点在x轴上的一椭圆与一双曲线有共同的焦点F1,F2,且|F1F2|=![]() ,椭圆的长半轴与双曲线实半轴之差为4,离心率之比为3∶7.
,椭圆的长半轴与双曲线实半轴之差为4,离心率之比为3∶7.
(1)求这两曲线的方程;
(2)若P为这两曲线的一个交点,求cos∠F1PF2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年9月16日05时,第19号台风“杜苏芮”的中心位于甲地,它以每小时30千米的速度向西偏北![]() 的方向移动,距台风中心
的方向移动,距台风中心![]() 千米以内的地区都将受到影响,若16日08时到17日08时,距甲地正西方向900千米的乙地恰好受台风影响,则
千米以内的地区都将受到影响,若16日08时到17日08时,距甲地正西方向900千米的乙地恰好受台风影响,则![]() 和
和![]() 的值分别为(附:
的值分别为(附: ![]() )( )
)( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经市场调查,某城市的一种小商品在过去的近20天内的销售量(件)与价格(元)均为时间t(天)的函数,且销售量近似满足g(t)=80﹣2t(件),价格近似满足于  (元).
(元).
(1)试写出该种商品的日销售额y与时间t(0≤t≤20)的函数表达式;
(2)求该种商品的日销售额y的最大值与最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com