练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    画出二元一次不等式2x＋3y－7＞0表示的平面区域．

    答案：
    解析：

    　　[解析]先画直线2x＋3y－7＝0(画成虚线)，取原点(0，0)代入2x＋3y－7中，因为2×0＋3×0－7＜0，所以二元一次不等式2x＋3y－7＞0表示的平面区域内的点与原点在直线2x＋3y－7＝0的两侧，即二元一次不等式2x＋3y－7＞0表示的平面区域在直线2x＋3y－7＝0的右上方．

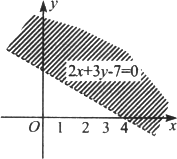
    　　[点评]由于二元一次不等式Ax＋By＋C＞0(或Ax＋By＋C＜0)表示的区域一定是直线Ax＋By＋C＝0的某一侧，要断定它究竟是哪一侧，可以取直线Ax＋By＋C＝0的一侧的一点，将它的坐标代入不等式，如果不等式成立，那么这一侧就是该不等式表示的区域；如果不等式不成立，那么直线的另一侧是该不等式表示的区域，如果直线不通过原点，一般取原点(0，0)来进行判断．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （必修3做）设计一个求
    1
    1×2
    +
    1
    2×3
    +…+
    1
    99×100
    的值的程序框图．
    （必修5做）请画出以A（3，-1）、B（-1，1）、C（1，3）为顶点的△ABC的区域（包括边界），写出表示该区域的二元一次不等式组，并求出以该区域为可行域的目标函数z=3x-2y的最大值与最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知x、y满足约束条件
    x≤4
    y≤4
    x+y≥4

    （1）画出该二元一次不等式组所表示的平面区域；
    （2）求目标函数z=x+4y的最大值；
    （3）求目标函数z=x-4y的最小值．

    查看答案和解析>>

    科目：高中数学 来源：高考总复习全解　数学　一轮复习·必修课程　（人教实验版）　B版 人教实验版　B版 题型：044

    画出下面二元一次不等式表示的平面区域．

    (1)x＋2y－3＞0；(2)2x－y－4≤0．

    查看答案和解析>>

    同步练习册答案