
ЃЈ1ЃЉЧѓЪ§Са{an}ЕФЭЈЯюЙЋЪНЃЛ
ЃЈ2ЃЉдкЪ§Са{bn}жаЃЌЖдШЮвте§ећЪ§nЃЌbnЁЄ![]() ЖМГЩСЂЃЌЩшSnЮЊЪ§Са{bn}ЕФЧАnЯюКЭЃЌБШНЯSnгы12ЕФДѓаЁЃЛ
ЖМГЩСЂЃЌЩшSnЮЊЪ§Са{bn}ЕФЧАnЯюКЭЃЌБШНЯSnгы12ЕФДѓаЁЃЛ
ЃЈ3ЃЉдкЕуСаAn(2n, )(nЁЪN*)жаЃЌЪЧЗёДцдкШ§ИіВЛЭЌЕуAkЁЂAlЁЂAmЃЌЪЙAkЁЂAlЁЂAmдквЛЬѕжБЯпЩЯЃПШєДцдкЃЌаДГівЛзщдквЛЬѕжБЯпЩЯЕФШ§ИіЕуЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
)(nЁЪN*)жаЃЌЪЧЗёДцдкШ§ИіВЛЭЌЕуAkЁЂAlЁЂAmЃЌЪЙAkЁЂAlЁЂAmдквЛЬѕжБЯпЩЯЃПШєДцдкЃЌаДГівЛзщдквЛЬѕжБЯпЩЯЕФШ§ИіЕуЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЃЈ1ЃЉНтЃКгЩ![]() =f(an)ЃЌЕУ
=f(an)ЃЌЕУ![]() =
= =
= .?
.?
Ёр![]() -
-![]() =4,МД{
=4,МД{![]() }ЪЧвд
}ЪЧвд![]() =1ЮЊЪзЯюЃЌ4ЮЊЙЋВюЕФЕШВюЪ§Са.?
=1ЮЊЪзЯюЃЌ4ЮЊЙЋВюЕФЕШВюЪ§Са.?
га![]() =1+ЃЈn-1ЃЉЁС4=4n-3ЃЌ?
=1+ЃЈn-1ЃЉЁС4=4n-3ЃЌ?
ЁпanЃО0,Ёрan=![]() . ?
. ?
ЃЈ2ЃЉНтЃКЁпbnЁЄ![]() ,?
,?
ЁрbnЁЄЃл(3n-1)+![]() Ѓн=bn(4n2-1)=1.?
Ѓн=bn(4n2-1)=1.?
Ёрbn=![]() =
=![]() (
(![]() -
-![]() ).?
).?
ЁрSn=b1+b2+Ё+bn?
=![]() Ѓл(1-
Ѓл(1-![]() )+(
)+(![]() -
-![]() )+Ё+(
)+Ё+(![]() -
-![]() )Ѓн?
)Ѓн?
=![]() (1-
(1-![]() )ЃМ
)ЃМ![]() .?
.?
ЁрSnЃМ![]() . ?
. ?
ЃЈ3ЃЉНтЃКЕуСаAn(2n,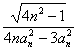 (nЁЪN*)жаВЛПЩФмгаЙВЯпЕФШ§ИіЕу. ?
(nЁЪN*)жаВЛПЩФмгаЙВЯпЕФШ§ИіЕу. ?
ИљОнЃЈ1ЃЉЃЌПЩЕУAn(2n,![]() )(nЁЪN*)ЃЌ?
)(nЁЪN*)ЃЌ?
Сюx=2n,y=![]() ,дђy=
,дђy=![]() ЃЈxЁн2ЃЉ.?
ЃЈxЁн2ЃЉ.?
ЕуЃЈx,yЃЉдкЧњЯпx2-y2=1(xЁн2,yЁн![]() )ЩЯЃЌ?
)ЩЯЃЌ?
ЫљвдAn(2n,![]() )дкЧњЯпx2-y2=1(xЁн2,yЁн
)дкЧњЯпx2-y2=1(xЁн2,yЁн![]() )ЩЯЃЌЖјжБЯпЗНГЬгыx2-y2=1СЊСЂзщГЩЕФЗНГЬзщзюЖргаСНзщВЛЭЌЕФНт.ЫљвджБЯпгыx2-y2=1зюЖргаСНИіНЛЕу.?
)ЩЯЃЌЖјжБЯпЗНГЬгыx2-y2=1СЊСЂзщГЩЕФЗНГЬзщзюЖргаСНзщВЛЭЌЕФНт.ЫљвджБЯпгыx2-y2=1зюЖргаСНИіНЛЕу.?
ЫљвдЕуСаAn(2n,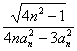 )(nЁЪN*)жаВЛПЩФмгаЙВЯпЕФШ§ИіЕу.
)(nЁЪN*)жаВЛПЩФмгаЙВЯпЕФШ§ИіЕу.


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
|
| 1 |
| Іа |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
 вбжЊКЏЪ§f(x)=
вбжЊКЏЪ§f(x)=
|
AЁЂ(
| ||||
BЁЂЃЈ
| ||||
CЁЂЃЈ
| ||||
DЁЂ[
|
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
| 2x-2-x | 2x+2-x |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
| x-1 | x+a |
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com