
已知圆 ,过点
,过点 作直线交圆C于
作直线交圆C于 两点,
两点, 面积的最大值为__________.
面积的最大值为__________.
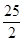
解析试题分析:根据题意可设出过点M(1,3)的直线l方程,利用点到直线的距离公式求得圆心(4,0)到l的距离,用弦心距、半弦长、半径组成的直角三角形进行计算转化,从而可得到△ABC面积的表达式,可求得其最大值. 设过点M(1,3)的直线方程为l:y-3=k(x-1),由x2-8x+y2-9=0得圆心C(4,0),半径r=5,设圆心C(4,0)到直线l的距离为d,点C在l上的射影为M,则d=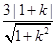 ,ABC
,ABC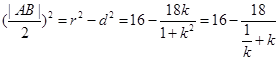 ,然后根据均值不等式得到了三角形面积的
,然后根据均值不等式得到了三角形面积的 为
为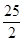
考点:直线方程与圆的方程的应用
点评:本题考查直线方程与圆的方程的应用,解决的方法利用弦心距、半弦长、半径组成的直角三角形进行计算,难点在于复杂的运算与化归,属于难题.


 科学实验活动册系列答案
科学实验活动册系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com