
【题目】在直角坐标系xOy中,曲线y=x2+mx–2与x轴交于A,B两点,点C的坐标为(0,1).当m变化时,解答下列问题:
(1)能否出现AC⊥BC的情况?说明理由;
(2)证明过A,B,C三点的圆在y轴上截得的弦长为定值.
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)设![]() ,由AC⊥BC得
,由AC⊥BC得![]() ;由根与系数的关系得
;由根与系数的关系得![]() ,矛盾,所以不存在;(2)求出过A,B,C三点的圆的圆心坐标和半径,即可得圆的方程,再利用垂径定理求弦长.
,矛盾,所以不存在;(2)求出过A,B,C三点的圆的圆心坐标和半径,即可得圆的方程,再利用垂径定理求弦长.
试题解析:(1)不能出现AC⊥BC的情况,理由如下:
设![]() ,
, ![]() ,则
,则![]() 满足
满足![]() ,所以
,所以![]() .
.
又C的坐标为(0,1),故AC的斜率与BC的斜率之积为![]() ,所以不能出现AC⊥BC的情况.
,所以不能出现AC⊥BC的情况.
(2)BC的中点坐标为(![]() ),可得BC的中垂线方程为
),可得BC的中垂线方程为![]() .
.
由(1)可得![]() ,所以AB的中垂线方程为
,所以AB的中垂线方程为![]() .
.
联立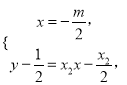 又
又![]() ,可得
,可得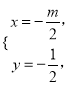
所以过A、B、C三点的圆的圆心坐标为(![]() ),半径
),半径![]()
故圆在y轴上截得的弦长为![]() ,即过A、B、C三点的圆在y轴上截得的弦长为定值.
,即过A、B、C三点的圆在y轴上截得的弦长为定值.


科目:高中数学 来源: 题型:
【题目】已知A(x1 , y1),B(x2 , y2)是函数f(x)= 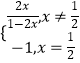 的图象上的任意两点(可以重合),点M在直线x=
的图象上的任意两点(可以重合),点M在直线x= ![]() 上,且
上,且 ![]() =
= ![]() .
.
(1)求x1+x2的值及y1+y2的值;
(2)已知S1=0,当n≥2时,Sn=f( ![]() )+f(
)+f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() ),求Sn .
),求Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知在四棱锥P﹣ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,PA= ![]() ,AB=1.AD=2.∠BAD=120°,E,F,G,H分别是BC,PB,PC,AD的中点.
,AB=1.AD=2.∠BAD=120°,E,F,G,H分别是BC,PB,PC,AD的中点.
(Ⅰ)求证:PH∥平面GED;
(Ⅱ)过点F作平面α,使ED∥平面α,当平面α⊥平面EDG时,设PA与平面α交于点Q,求PQ的长.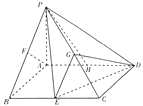
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,已知定义在R上的函数
,已知定义在R上的函数![]() 在区间
在区间![]() 内有一个零点
内有一个零点![]() ,
, ![]() 为
为![]() 的导函数.
的导函数.
(Ⅰ)求![]() 的单调区间;
的单调区间;
(Ⅱ)设![]() ,函数
,函数![]() ,求证:
,求证: ![]() ;
;
(Ⅲ)求证:存在大于0的常数![]() ,使得对于任意的正整数
,使得对于任意的正整数![]() ,且
,且![]() 满足
满足![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】集合A={x|1≤x≤5},B={x|2≤x≤6},
(1)若x∈A,y∈B且均为整数,求x>y的概率.
(2)若x∈A,y∈B且均为实数,求x>y的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg), 其频率分布直方图如下:

(1)记A表示事件“旧养殖法的箱产量低于50 kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50 kg | 箱产量≥50 kg | |
旧养殖法 | ||
新养殖法 |
(3)根据箱产量的频率分布直方图,对这两种养殖方法的优劣进行比较.
附:
P( | 0.050 0.010 0.001 |
k | 3.841 6.635 10.828 |
![]() .
. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直(其中
垂直(其中![]() 为自然对数的底数).
为自然对数的底数).
(I)求![]() 的解析式及单调递减区间;
的解析式及单调递减区间;
(II)是否存在常数![]() ,使得对于定义域内的任意
,使得对于定义域内的任意![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com