
【题目】集合A={x|1≤x≤5},B={x|2≤x≤6},
(1)若x∈A,y∈B且均为整数,求x>y的概率.
(2)若x∈A,y∈B且均为实数,求x>y的概率.
【答案】
(1)解:设事件A:”x>y”
基本事件有:(1,2),(1,3),(1,4),(1,5),(1,6),(2,2),(2,3),(2,4),(2,5),(2,6),(3,2),(3,3),(3,4),(3,5),(3,6),(4,2),(4,3),(4,4),(4,5),(4,6),(5,2),(5,3)(5,4)(5,5)(5,6)共25个.(1)其中事件A包含的基本事件有(3,2),(4,2),(4,3),(5,2),(5,3),(5,4)共6个.
∴P(A)= ![]()
(2)解:设事件B:”x>y”(画图
总基本事件{(x,y)| ![]() },其对应的平面区域如图中矩形部分所示
},其对应的平面区域如图中矩形部分所示
其中事件B:”x>y”{(x,y)|  }
}
所围成的面积为图中阴影部份.
E的坐标为(2,2),F的坐标为(5,5),B的坐标为(2,5)
P(B)= ![]() =
= ![]() =
= ![]()

【解析】(1)列举出所有满足“x∈A,y∈B,且均为整数”的基本事件的总个数,及其中满足条件x>y的基本事件的个数,代入古典概型概率计算公式,即可得到答案.(2)画出满足x∈A,y∈B,且均为实数的基本事件对应的平面区域,及其中满足条件x>y的平面区域,代入几何概型概率计算公式,即可得到答案.
【考点精析】掌握几何概型是解答本题的根本,需要知道几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直接AB与平面MNQ不平行的是
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 上一点,
上一点, ![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
, ![]() 到
到![]() 的准线的距离为
的准线的距离为![]() ,且
,且![]() 的最小值为
的最小值为![]() .
.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)直线![]() 交
交![]() 于点
于点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() ,线段
,线段![]() 的中点分别为
的中点分别为![]() ,若
,若![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求证:直线
,求证:直线![]() 恒过定点.
恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线y=x2+mx–2与x轴交于A,B两点,点C的坐标为(0,1).当m变化时,解答下列问题:
(1)能否出现AC⊥BC的情况?说明理由;
(2)证明过A,B,C三点的圆在y轴上截得的弦长为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在长方体ABCD﹣A1B1C1D1中,AB=5,AD=8,AA1=4,M为B1C1上一点且B1M=2,点N在线段A1D上,A1D⊥AN. 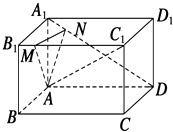
(1)求直线A1D与AM所成角的余弦值;
(2)求直线AD与平面ANM所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的离心率为
的离心率为![]() ,圆心在
,圆心在![]() 轴的正半轴上的圆
轴的正半轴上的圆![]() 与双曲线的渐近线相切,且圆
与双曲线的渐近线相切,且圆![]() 的半径为2,则以圆
的半径为2,则以圆![]() 的圆心为焦点的抛物线的标准方程为( )
的圆心为焦点的抛物线的标准方程为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】1927年德国汉堡大学的学生考拉兹提出一个猜想:对于每一个正整数,如果它是奇数,对它乘3再加1,如果它是偶数,对它除以2,这样循环,最终结果都能得到1.该猜想看上去很简单,但有的数学家认为“该猜想任何程度的解决都是现代数学的一大进步,将开辟全新的领域至于如此简单明了的一个命题为什么能够开辟一个全新的领域,这大概与它其中蕴含的奇偶归一思想有关.如图是根据考拉兹猜想设计的一个程序框图,则①处应填写的条件及输出的结果![]() 分别为
分别为
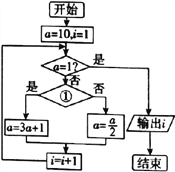
A. ![]() 是偶数?;6 B.
是偶数?;6 B. ![]() 是偶数?;8
是偶数?;8
C. ![]() 是奇数?;5 D.
是奇数?;5 D. ![]() 是奇数?;7
是奇数?;7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() =(2sinx,cosx+sinx),
=(2sinx,cosx+sinx), ![]() =(cosx,cosx﹣sinx),f(x)=
=(cosx,cosx﹣sinx),f(x)= ![]()
![]() .
.
(1)求函数f(x)的单调区间;
(2)若关于x的方程f(x)﹣m=0(m∈R)在区间(0, ![]() )内有两个不相等的实数根x1 , x2 , 记t=mcos(x1+x2),求实数t的取值范围.
)内有两个不相等的实数根x1 , x2 , 记t=mcos(x1+x2),求实数t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com