【题目】已知tanα=2．
（1）求 
的值；
（2）若α∈（0， 
），求sin（α﹣ 
）的值．
【答案】
（1）解：由tanα=2 知，cosα≠0，∴ 
= 
= 
（2）解：由tanα=2= 
，得sinα=2cosα，再根据sin2α+cos2α=1，α∈（0， 
），
求得cosα= 
，sinα= 
，
∴sin（α﹣ 
）=sinαcos ﹣cosαsin = 
﹣ 
= 
【解析】（1）利用同角三角函数的基本关系，求得要求式子的值．（2）利用同角三角函数的基本关系求得cosα 和sinα的值，再利用两角差的正弦公式求得sin（α﹣ ）的值．
【考点精析】通过灵活运用同角三角函数基本关系的运用和两角和与差的余弦公式，掌握同角三角函数的基本关系：
；
;（3） 倒数关系：
；两角和与差的余弦公式：
即可以解答此题．
名校课堂系列答案科目：高中数学 来源： 题型：
【题目】如图，已知在四棱锥P﹣ABCD中，底面ABCD是平行四边形，PA⊥平面ABCD，PA= 
，AB=1．AD=2．∠BAD=120°，E，F，G，H分别是BC，PB，PC，AD的中点．
（Ⅰ）求证：PH∥平面GED；
（Ⅱ）过点F作平面α，使ED∥平面α，当平面α⊥平面EDG时，设PA与平面α交于点Q，求PQ的长．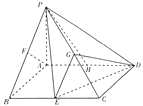
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】集合A={x|1≤x≤5}，B={x|2≤x≤6}，
（1）若x∈A，y∈B且均为整数，求x＞y的概率．
（2）若x∈A，y∈B且均为实数，求x＞y的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取了100个网箱，测量各箱水产品的产量（单位：kg）, 其频率分布直方图如下：
（1）记A表示事件“旧养殖法的箱产量低于50 kg”，估计A的概率；
（2）填写下面列联表，并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关：
箱产量＜50 kg | 箱产量≥50 kg | |
旧养殖法 | ||
新养殖法 |
（3）根据箱产量的频率分布直方图，对这两种养殖方法的优劣进行比较.
附：
P（ | 0.050 0.010 0.001 |
k | 3.841 6.635 10.828 |
. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知f（x）= 
x3﹣2ax2﹣3x（a∈R）． （Ⅰ）若f（x）在区间（﹣1，1）内为减函数，求实数a的取值范围；
（Ⅱ）对于实数a的不同取值，试讨论y=f（x）在（﹣1，1）内的极值点的个数．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，曲线
在点
处的切线与直线
垂直（其中
为自然对数的底数）．
（I）求
的解析式及单调递减区间；
（II）是否存在常数
，使得对于定义域内的任意
恒成立？若存在，求出
的值；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】随机询问某大学40名不同性别的大学生在购买食物时是否读营养说明，得到如下列联表：
男 | 女 | 总计 | |
读营养说明 | 16 | 8 | 24 |
不读营养说明 | 4 | 12 | 16 |
总计 | 20 | 20 | 40 |
（1）根据以上列联表进行独立性检验，能否在犯错误的概率不超过0.01的前提下认为性别与是否读营养说明之间有关系？
（2）从被询问的16名不读营养说明的大学生中，随机抽取2名学生，求抽到男生人数
的分布列及其均值（即数学期望）．
（注： 
，其中
为样本容量）
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
