
【题目】已知f(x)= ![]() x3﹣2ax2﹣3x(a∈R). (Ⅰ)若f(x)在区间(﹣1,1)内为减函数,求实数a的取值范围;
x3﹣2ax2﹣3x(a∈R). (Ⅰ)若f(x)在区间(﹣1,1)内为减函数,求实数a的取值范围;
(Ⅱ)对于实数a的不同取值,试讨论y=f(x)在(﹣1,1)内的极值点的个数.
【答案】解:(Ⅰ)对函数g(x)求导得,f'(x)=2x2﹣4ax﹣3, ∵f(x)在区间(﹣1,1)内为减函数,
∴f'(x)≤0在x∈(﹣1,1)上恒成立,
结合二次函数的图象和性质,
问题等价为: 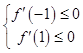 ,即
,即 ![]() ,
,
解得﹣ ![]() ≤a≤
≤a≤ ![]() ,
,
∴实数a的取值范围为[﹣ ![]() ,
, ![]() ],
],
(Ⅱ)当a<﹣ ![]() 时,f′(﹣1)=4a﹣1<0,f′(1)=﹣4a﹣1>0
时,f′(﹣1)=4a﹣1<0,f′(1)=﹣4a﹣1>0
∴f(x)在(﹣1,1)内有且只有一个极小值点,
当a> ![]() 时,f′(﹣1)=4a﹣1>0,f′(1)=﹣4a﹣1<0,
时,f′(﹣1)=4a﹣1>0,f′(1)=﹣4a﹣1<0,
∴f(x)在(﹣1,1)内有且只有一个极大值点,
当﹣ ![]() ≤a≤
≤a≤ ![]() 时,由(Ⅰ)可知在区间(﹣1,1)上为减函数,
时,由(Ⅰ)可知在区间(﹣1,1)上为减函数,
∴f(x)在区间(﹣1,1)内没有极值点.
综上可知,当a<﹣ ![]() 或a>
或a> ![]() 时,函数在区间(﹣1,1)内的极值点个数为1;当﹣
时,函数在区间(﹣1,1)内的极值点个数为1;当﹣ ![]() ≤a≤
≤a≤ ![]() 时,在区间(﹣1,1)内的极值点个数为0
时,在区间(﹣1,1)内的极值点个数为0
【解析】(Ⅰ)先求出导函数,根据题意问题等价为g'(x)≤0在x∈(﹣1,1)上恒成立,再根据二次函数的性质转化为: ![]() ,解出即可,(Ⅱ)分类讨论.利用导数的正负,即可得出y=f(x)在(﹣1,1)内的极值点的个数.
,解出即可,(Ⅱ)分类讨论.利用导数的正负,即可得出y=f(x)在(﹣1,1)内的极值点的个数.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减,以及对函数的极值与导数的理解,了解求函数
在这个区间单调递减,以及对函数的极值与导数的理解,了解求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的离心率为
的离心率为![]() ,圆心在
,圆心在![]() 轴的正半轴上的圆
轴的正半轴上的圆![]() 与双曲线的渐近线相切,且圆
与双曲线的渐近线相切,且圆![]() 的半径为2,则以圆
的半径为2,则以圆![]() 的圆心为焦点的抛物线的标准方程为( )
的圆心为焦点的抛物线的标准方程为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在x∈[ ![]() ,2]上,函数f(x)=x2+px+q与g(x)=
,2]上,函数f(x)=x2+px+q与g(x)= ![]() +
+ ![]() 在同一点取得相同的最小值,那么f(x)在x∈[
在同一点取得相同的最小值,那么f(x)在x∈[ ![]() ,2]上的最大值是( )
,2]上的最大值是( )
A.![]()
B.4
C.8
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知Sn是等差数列{an}的前n项和,公差为d,且S2015>S2016>S2014 , 下列五个命题:①d>0;②S4029>0;③S4030<0;④数列{Sn}中的最大项为S2015;⑤|a2015|>|a2016|.
其中正确结论的序号是 . (写出所有正结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , 等比数列{bn}的各项均为正数,满足:a1=b1=1,a5=b3 , 且S3=9.
(1)求数列{an}和{bn}的通项公式;
(2)求 ![]() +
+ ![]() +…+
+…+ ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的左、右焦点分别为F1、F2 , 短轴两个端点为A、B,且四边形F1AF2B是边长为2的正方形.
的左、右焦点分别为F1、F2 , 短轴两个端点为A、B,且四边形F1AF2B是边长为2的正方形. 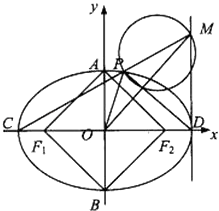
(1)求椭圆的方程;
(2)若C、D分别是椭圆长的左、右端点,动点M满足MD⊥CD,连接CM,交椭圆于点P.证明: ![]() 为定值.
为定值.
(3)在(2)的条件下,试问x轴上是否存异于点C的定点Q,使得以MP为直径的圆恒过直线DP、MQ的交点,若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com