
【题目】已知双曲线![]() 的离心率为
的离心率为![]() ,圆心在
,圆心在![]() 轴的正半轴上的圆
轴的正半轴上的圆![]() 与双曲线的渐近线相切,且圆
与双曲线的渐近线相切,且圆![]() 的半径为2,则以圆
的半径为2,则以圆![]() 的圆心为焦点的抛物线的标准方程为( )
的圆心为焦点的抛物线的标准方程为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cos
=(cos ![]() x,sin
x,sin ![]() x),
x), ![]() =(cos
=(cos ![]() x,﹣sin
x,﹣sin ![]() x),且x∈[0,
x),且x∈[0, ![]() ].求:
].求:
(1)![]() 及
及 ![]() ;
;![]()
(2)若f(x)= ![]() ﹣2λ
﹣2λ ![]() 的最小值是﹣
的最小值是﹣ ![]() ,求λ的值.
,求λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+1(a>0),g(x)=x3+bx.
(1)若曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处具有公共切线,求a,b的值;
(2)当a=3,b=-9时,若函数f(x)+g(x)在区间[k,2]上的最大值为28,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=-![]() x3+x2+(m2-1)x(x∈R),其中m>0.
x3+x2+(m2-1)x(x∈R),其中m>0.
(1)当m=1时,求曲线y=f(x)在点(1,f(1))处的切线斜率;
(2)求函数的单调区间与极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 为菱形,
为菱形, ![]() ,
, ![]() 与
与![]() 相交于点
相交于点![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() 为
为![]() 中点.
中点.
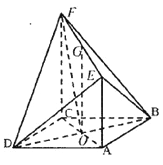
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的正弦值;
的正弦值;
(Ⅲ)当直线![]() 与平面
与平面![]() 所成角为
所成角为![]() 时,求异面直线
时,求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)当![]() 时,求
时,求![]() 在
在![]() 处的切线方程;
处的切线方程;
(Ⅱ)若![]() 且函数
且函数![]() 有且仅有一个零点,求实数
有且仅有一个零点,求实数![]() 的值;
的值;
(Ⅲ)在(Ⅱ)的条件下,若![]() 时,
时, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在正方形![]() 中,点
中,点![]() 分别是
分别是![]() 的中点,
的中点,![]() 与
与![]() 交于点
交于点![]() ,点
,点![]() 分别在线段
分别在线段![]() 上,且
上,且![]() .将
.将![]() 分别沿
分别沿![]() 折起,使点
折起,使点![]() 重合于点
重合于点![]() ,如图2所示.
,如图2所示.
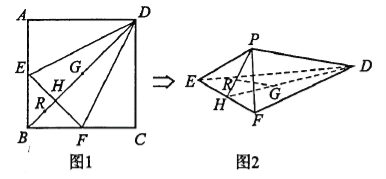
(1)求证:![]() 平面
平面![]() ;
;
(2)若正方形![]() 的边长为4,求三棱锥
的边长为4,求三棱锥![]() 的内切球的半径.
的内切球的半径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若方程![]() 所表示的曲线为C,给出下列四个命题:
所表示的曲线为C,给出下列四个命题:
①若C为椭圆,则1<t<4且t≠![]() ;
;
②若C为双曲线,则t>4或t<1;
③曲线C不可能是圆;
④若C表示椭圆,且长轴在x轴上,则1<t<![]() .
.
其中正确的命题是________(把所有正确命题的序号都填在横线上).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com