
 为了美化校园环境,学校打算在兰蕙广场上建造一个绚丽多彩的矩形花园,中间有三个完全一样的矩形花坛,每个花坛面积均为294平方米,花坛四周的过道均为2米,如图所示,设矩形花坛的长为x,宽为y,整个矩形花园面积为S.
为了美化校园环境,学校打算在兰蕙广场上建造一个绚丽多彩的矩形花园,中间有三个完全一样的矩形花坛,每个花坛面积均为294平方米,花坛四周的过道均为2米,如图所示,设矩形花坛的长为x,宽为y,整个矩形花园面积为S.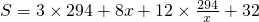 =
=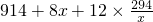 x∈(0,+∞)
x∈(0,+∞)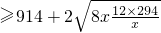 =914+2×4×6×7=1250
=914+2×4×6×7=1250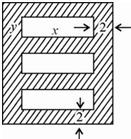
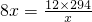 ,即x=21时,等号成立.
,即x=21时,等号成立.

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com