
【题目】已知直线![]() :
: ![]() 恒过定点
恒过定点![]() ,圆
,圆![]() 经过点
经过点![]() 和点
和点![]() ,且圆心在直线
,且圆心在直线![]() 上.
上.
(1)求定点![]() 的坐标;
的坐标;
(2)求圆![]() 的方程;
的方程;
(3)已知点![]() 为圆
为圆![]() 直径的一个端点,若另一个端点为点
直径的一个端点,若另一个端点为点![]() ,问:在
,问:在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 为直角三角形,若存在,求出
为直角三角形,若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)直线过定点问题,应将直线![]() :
: ![]() 的方程中含
的方程中含![]() 的项合并,变为
的项合并,变为![]() ,解方程组
,解方程组![]() 即可求定点坐标;(2)方法一:设圆
即可求定点坐标;(2)方法一:设圆![]() 的一般方程为
的一般方程为![]() ,其圆心为
,其圆心为![]() ,由条件可得关于
,由条件可得关于![]() 三元方程组,解方程组可求解;方法二:设圆的方程为标准方程。(3)圆心C为
三元方程组,解方程组可求解;方法二:设圆的方程为标准方程。(3)圆心C为![]() 的中点,由中点坐标公式求点
的中点,由中点坐标公式求点![]() 的坐标。点M到圆心C距离大于半径,所以点M在圆C外。故
的坐标。点M到圆心C距离大于半径,所以点M在圆C外。故![]() 或
或![]() 为直角,两邻边垂直,斜率乘积为-1,可求m的值。
为直角,两邻边垂直,斜率乘积为-1,可求m的值。
试题解析:(1)由![]() 得,
得, ![]() ,
,
令![]() ,得
,得![]() ,即定点
,即定点![]() 的坐标为
的坐标为![]() .
.
(2)设圆![]() 的方程为
的方程为![]() ,
,
由条件得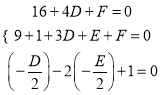 ,解得
,解得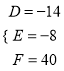 .
.
所以圆![]() 的方程为
的方程为![]() .
.
(3)圆![]() 的标准方程为
的标准方程为![]() ,
, ![]() ,
,
设点![]() 关于圆心
关于圆心![]() 的对称点为
的对称点为![]() ,则有
,则有![]() ,
,
解得![]() ,
, ![]() ,故点
,故点![]() 的坐标为
的坐标为![]() .
.
因为![]() 在圆外,所以点
在圆外,所以点![]() 不能作为直角三角形的顶点,
不能作为直角三角形的顶点,
若点![]() 为直角三角形的顶点,则有
为直角三角形的顶点,则有![]() ,
, ![]() ,
,
若点![]() 是直角三角形的顶点,则有
是直角三角形的顶点,则有![]() ,
, ![]() ,
,
综上, ![]() 或
或![]() .
.
所以![]() ,
,
所以![]() .
.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】在10名学生中,男生有x名,现从10名学生中任选6人去参加某项活动:①至少有1名女生;②5名男生,1名女生;③3名男生,3名女生.若要使①为必然事件,②为不可能事件,③为随机事件,则x=( )
A.5B.6C.3或4D.5或6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() 为椭圆上一点(在
为椭圆上一点(在![]() 轴上方),连结
轴上方),连结![]() 并延长交椭圆于另一点
并延长交椭圆于另一点![]() ,设
,设![]() .
.

(1)若点![]() 的坐标为
的坐标为![]() ,且
,且![]() 的周长为8,求椭圆
的周长为8,求椭圆![]() 的方程;
的方程;
(2)若![]() 垂直于
垂直于![]() 轴,且椭圆
轴,且椭圆![]() 的离心率
的离心率![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—1:几何证明选讲
如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B、C两点,圆心O在∠PAC的内部,点M是BC的中点.
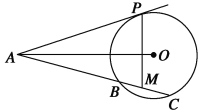
(1)证明:A、P、O、M四点共圆;
(2)求∠OAM+∠APM的大小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运输队接到给灾区运送物资的任务,该运输队有8辆载重为![]() 的
的![]() 型卡车,6辆载重为
型卡车,6辆载重为![]() 的
的![]() 型卡车,10名驾驶员,要求此运输队每天至少运送
型卡车,10名驾驶员,要求此运输队每天至少运送![]() 救灾物资.已知每辆卡车每天往返的次数为
救灾物资.已知每辆卡车每天往返的次数为![]() 型卡车16次,
型卡车16次, ![]() 型卡车12次.每辆卡车每天往返的成本为
型卡车12次.每辆卡车每天往返的成本为![]() 型卡车240元,
型卡车240元, ![]() 型卡车378元.问每天派出
型卡车378元.问每天派出![]() 型卡车与
型卡车与![]() 型卡车各多少辆,运输队所花的成本最低?
型卡车各多少辆,运输队所花的成本最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的中心在坐标原点![]() ,焦点在
,焦点在![]() 轴上,短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的顶点.过右焦点
轴上,短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的顶点.过右焦点![]() 与
与![]() 轴不垂直的直线
轴不垂直的直线![]() 交椭圆于
交椭圆于![]() 两点.
两点.
(1)求椭圆的方程;
(2)当直线![]() 的斜率为1时,求
的斜率为1时,求![]() 的面积;
的面积;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得以
,使得以![]() 为邻边的平行四边形是菱形?若存在,求出
为邻边的平行四边形是菱形?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市![]() 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.
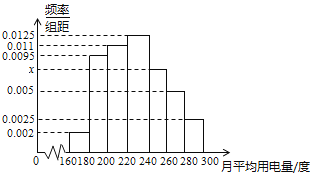
(1)求直方图中![]() 的值;
的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为![]() ,
, ![]() ,
, ![]() ,
, ![]() 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取![]() 户居民,则月平均用电量在
户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在扶贫活动中,为了尽快脱贫(无债务)致富,企业甲将经营状况良好的某种消费品专卖店以5.8万元的优惠价格转让给了尚有5万元无息贷款没有偿还的小型企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月最低生活费的开支3 600元后,逐步偿还转让费(不计息).在甲提供的资料中:①这种消费品的进价为每件14元;②该店月销量Q(百件)与销售价格P(元)的关系如图所示;③每月需各种开支2 000元.
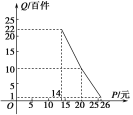
(1)当商品的价格为每件多少元时,月利润扣除职工最低生活费的余额最大?并求最大余额;
(2)企业乙只依靠该店,最早可望在几年后脱贫?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com