练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    若等比数列{an}的各项均为正数，且a10a11+a9a12=2e5，则lna1+lna2+…lna20=
     
    ．
    考点：等比数列的性质,对数的运算性质
    专题：等差数列与等比数列
    分析：直接由等比数列的性质结合已知得到a10a11=e5，然后利用对数的运算性质化简后得答案．
    解答： 解：∵数列{an}为等比数列，且a10a11+a9a12=2e5，
    ∴a10a11+a9a12=2a10a11=2e5，
    则a10a11=e5，
    ∴lna1+lna2+…lna20=ln(a1a2…a20)=ln(a10a11)10
    =ln（e5）10=lne50=50．
    故答案为：50．
    点评：本题考查了等比数列的运算性质，考查对数的运算性质，考查了计算能力，是基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如果若干个函数的图象经过平移后能够重合，则称这些函数为“同簇函数”．给出下列函数：
    ①f（x）=sinxcosx，
    ②f（x）=
    		2
    sin2x+2，
    ③f（x）=2sin（x+
    π
    4
    ），
    ④f（x）=sinx-
    		3
    cosx，
    其中属于“同簇函数”的是（　　）
    A、①②B、①④C、②③D、③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知f（x）是定义在R上的奇函数，当x≥0时，f（x）=x2-3x，则函数g（x）=f（x）-x+3的零点的集合为（　　）
    A、{1，3}
    B、{-3，-1，1，3}
    C、{2-
    		7
    ，1，3}
    D、{-2-
    		7
    ，1，3}

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知数列{an}满足a1=1，an+1=3an+1．
    （Ⅰ）证明{an+
    1
    2
    }是等比数列，并求{an}的通项公式；
    （Ⅱ）证明：
    1
    a1
    +
    1
    a2
    +…+
    1
    an
    ＜
    3
    2
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    甲、乙两位同学从A、B、C、D共4所高校中，任选两所参加自主招生考试（并且只能选两所高校），但同学甲特别喜欢A高校，他除选A高校外，再在余下的3所中随机选1所；同学乙对4所高校没有偏爱，在4所高校中随机选2所．
    （1）求乙同学选中D高校的概率；
    （2）求甲、乙两名同学恰有一人选中D高校的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设函数f（x）=alnx+
    x-1
    x+1
    ，其中a为常数．
    （Ⅰ）若a=0，求曲线y=f（x）在点（1，f（1））处的切线方程；
    （Ⅱ）讨论函数f（x）的单调性．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

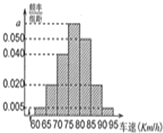    2014年“五一节”期间，高速公路车辆较多，交警部门通过路面监控装置抽样调查某一山区路段汽车行驶速度，采用的方法是：按到达监控点先后顺序，每隔50辆抽取一辆，总共抽取120辆，分别记下其行车速度，将行车速度（km/h）分成七段[60，65），[65，70），[70，75），[75，80），[80，85），[85，90），[90，95）后得到如图所示的频率分布直方图，据图解答下列问题：
    （Ⅰ）求a的值，并说明交警部门采用的是什么抽样方法？
    （Ⅱ）求这120辆车行驶速度的众数和中位数的估计值（精确到0.1）；
    （Ⅲ）若该路段的车速达到或超过90km/h即视为超速行驶，试根据样本估计该路段车辆超速行驶的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，内角A，B，C所对的边分别为a，b，c，已知a-c=
    		6
    6
    b，sinB=
    		6
    sinC，
    （Ⅰ）求cosA的值；
    （Ⅱ）求cos（2A-
    π
    6
    ）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    等比数列{an}中，a3=7，前3项和S3=21，则数列{an}的公比为
     
    ．

    查看答案和解析>>

    同步练习册答案