
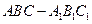 中,
中,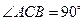 ,
,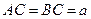 ,
,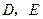 分别为棱
分别为棱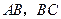 的中点,
的中点,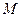 为棱
为棱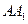 上的点,二面角
上的点,二面角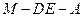 为
为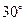 .
.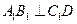 ;
;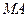 的长,并求点
的长,并求点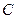 到平面
到平面 的距离.
的距离.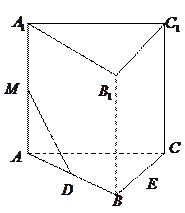
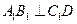
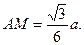 C到平面MDE的距离与A到平面MDE的距离相等,为
C到平面MDE的距离与A到平面MDE的距离相等,为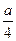
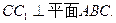
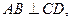
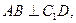
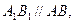
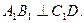
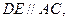
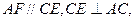
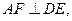
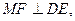
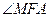 为二面角
为二面角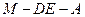 的平面角,
的平面角,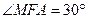 .
.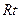 △MAF中,
△MAF中,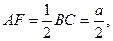
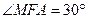 ,
,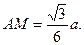
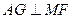 ,垂足为G.
,垂足为G.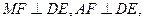
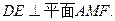
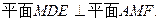
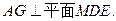
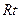 △GAF中,
△GAF中,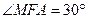 ,AF=
,AF=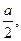
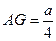 ,即A到平面MDE的距离为
,即A到平面MDE的距离为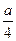 .
.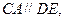 ∴
∴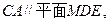
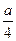 ,
,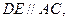
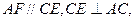
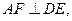
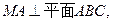
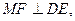
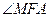 为二面角
为二面角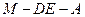 的平面角,
的平面角,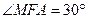 .
.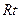 △MAF中,
△MAF中,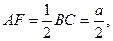
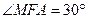 ,
,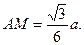
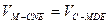 ,
,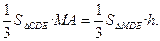
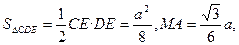
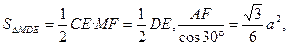
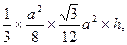
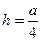 ,即C到平面MDE的距离相等,为
,即C到平面MDE的距离相等,为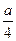


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源:不详 题型:解答题
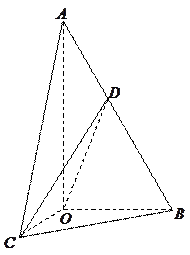
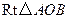 中,
中,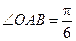 ,斜边
,斜边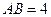 .
.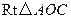 可以通过
可以通过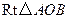 以直线
以直线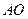 为轴旋转得到,且二面角
为轴旋转得到,且二面角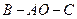 是直二面角.动点
是直二面角.动点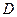 的斜边
的斜边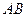 上.
上.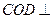 平面
平面 ;
;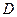 为
为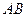 的中点时,求异面直线
的中点时,求异面直线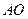 与
与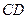 所成角的大小;
所成角的大小;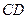 与平面
与平面 所成角的最大值.
所成角的最大值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
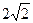 .
. (2)在线段
(2)在线段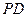 上是否存在一点
上是否存在一点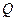 ,使
,使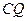 与平面
与平面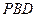 所成的角的正弦值为
所成的角的正弦值为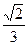 ,若存在,
,若存在,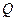 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
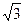 ,⊙O为其内切圆,D为BC的中点,将三角形ACD沿AD折叠,使二面角B-AD-C成直二面角,则⊙O上的圆弧扫过的曲面面积为____________.
,⊙O为其内切圆,D为BC的中点,将三角形ACD沿AD折叠,使二面角B-AD-C成直二面角,则⊙O上的圆弧扫过的曲面面积为____________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com