
分析 求出抛物线的准线为x=-1,焦点为F(1,0).根据对称性可得△FAB是等腰直角三角形,从而算出A、B的坐标,将其代入双曲线方程,解关于a的等式即可得到实数a的值.
解答 解: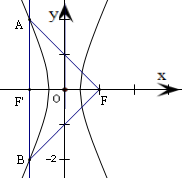 ∵抛物线的方程为y2=4x,
∵抛物线的方程为y2=4x,
∴抛物线的准线为x=-1,焦点为F(1,0).
又∵直线x=-1交双曲线$\frac{{x}^{2}}{{a}^{2}}$-y2(a>0)于A、B两点,
△FAB为直角三角形.
∴△FAB是等腰直角三角形,AB边上的高FF'=2,
由此可得A(-1,2)、B(-1,-2),如图所示
将点A或点B的坐标代入双曲线方程,得$\frac{1}{{a}^{2}}$-4=1,
解之得a=$\frac{\sqrt{5}}{5}$(舍负),
故答案为:$\frac{\sqrt{5}}{5}$.
点评 本题给出抛物线与双曲线满足的条件,在已知抛物线的方程情况下求双曲线的标准方程.着重考查了抛物线、双曲线的标准方程与简单几何性质等知识,属于中档题.


科目:高中数学 来源: 题型:解答题
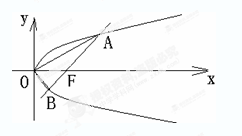 过直角坐标平面xOy中的抛物线y2=2px的焦点F作一条倾斜角为$\frac{π}{4}$的直线与抛物线相交于A,B两点.
过直角坐标平面xOy中的抛物线y2=2px的焦点F作一条倾斜角为$\frac{π}{4}$的直线与抛物线相交于A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 有5位工人在某天生产同一零件,所生产零件个数的茎叶图如图所示,已知它们生产零件的平均数为10,标准差为$\sqrt{2}$,则|x-y|的值为( )
有5位工人在某天生产同一零件,所生产零件个数的茎叶图如图所示,已知它们生产零件的平均数为10,标准差为$\sqrt{2}$,则|x-y|的值为( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
| A. | 10.38 | B. | 12.38 | C. | 13.08 | D. | 13.28 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 8 | B. | 20+8$\sqrt{2}$ | C. | 16 | D. | 24+8$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com