分析:(1)先建立空间直角坐标系,求出各点的坐标,直接根据PC⊥AB对应的数量积为0即可求出点P的位置;
(2)先根据条件求出点P的坐标,再求出两个平面的法向量,代入向量的夹角计算公式即可求出结论;
(3)直接利用公式h=|
|•cos<
,>计算即可.
解答: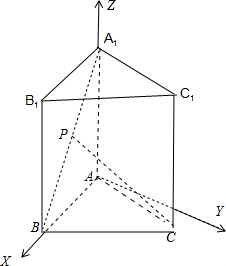
解:以A为原点,AB为X轴,过点A且与AB垂直的直线为Y轴,AA
1为Z轴,建立空间直角坐标系A-XYZ;
则B(a,0,0),A
1(0,0,a);C(
,
a,0),P(x,0,x);
(1)由
•=0⇒(x-
,-
a,z)•(a,0,0)=0,
即(x-
)•a=0,x=
,
所以:P为AB的中点;
即
=1时,PC⊥AB;
(2)当
=时,即
=
,
得(x,0,z-a)=
(a-x,0,-z)
⇒
,
所以:P(
,0,
).
设平面PAC的一个法向量
=(b,c,d)
则
⇒
即
| | (b,c,d)• (,0,)=0 | | (b,c,d)•(,,0)=0 |
| |
⇒
;
取b=3,则c=-
,d=-2.
∴
=(3,-
,-2),
又平面ABC的一个法向量
=(0,0,1),
∴cos<
,>=
=
=-
.
∴二面角P-AC-B的大小180°-120°=60°.
(3)设C
1到平面PAC的距离为h,
则h=|
|•cos<
,>=
=
=
.
故C
1到平面PAC的距离为
.
点评:本题是对立体几何知识的综合考察,其中涉及到点到面的距离,二面角,线线垂直等知识,属于综合性很强的题目,要认真分析.

 如图,已知正三棱柱ABC-A1B1C1的各条棱长都为a,P为A1B上的点.
如图,已知正三棱柱ABC-A1B1C1的各条棱长都为a,P为A1B上的点. 解:以A为原点,AB为X轴,过点A且与AB垂直的直线为Y轴,AA1为Z轴,建立空间直角坐标系A-XYZ;
解:以A为原点,AB为X轴,过点A且与AB垂直的直线为Y轴,AA1为Z轴,建立空间直角坐标系A-XYZ;

 如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为线段A1B上的动点.
如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为线段A1B上的动点. 如图,已知正三棱柱ABC-A1B1C1的底面边长为2cm,高位5cm,一质点自A点出发,沿着三棱柱的侧面绕行两周到达A1点的最短路线的长为
如图,已知正三棱柱ABC-A1B1C1的底面边长为2cm,高位5cm,一质点自A点出发,沿着三棱柱的侧面绕行两周到达A1点的最短路线的长为 (2011•重庆三模)如图,已知正三棱柱ABC-A1B1C1的所有棱长均为a,截面AB1C和A1BC1相交于DE,则三棱锥B-B1DE的体积为
(2011•重庆三模)如图,已知正三棱柱ABC-A1B1C1的所有棱长均为a,截面AB1C和A1BC1相交于DE,则三棱锥B-B1DE的体积为