解:(1)证明:∵x
1,x
2是f(x)=
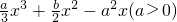
的两个极值点,
∴x
1,x
2是f′(x)=ax
2+bx-a
2的两个根,
∴x
1x
2=-a,…(2分)
∴由条件|x
1|+|x
2|=1及基本不等式可得
2
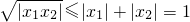
,
∴
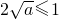
,
∴
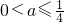
.…(5分)
(2)由条件可得x
12+x
22+2|x
1x
2|=1,
即(x
1+x
2)
2-2x
1x
2+2|x
1x
2|=1,
∴
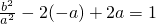
,
∴b
2=(1-4a)a
2,
令h(a)=(1-4a)a
2=-4a
3+a
2,
则h′(x)=-2a(6a-1).
∵
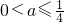
,
∴
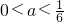
时,h′(a)>0;
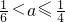
时,h′(a)<0.
∴h(a)在a=

处取得最大值
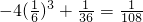
,
而
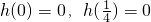
,
故h(a)在[0,

]上的最大值为
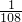
,
也就是在(0,

]上的最大值为
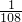
,此时a=

,
∴
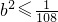
,即|b|≤
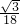
. …(10分)
(3)g(x)=f′(x)-a(x-x
1)(x-x
2)-a(x-x
1)(x-x
2-1)(12分)
由条件x-x
1>0,
∵x
1x
2=-a<0,x
1<0,
∴x
2>0,x<1,
∴x-x
2-1<0,
∴|g(x)|=a(x-x
1)(1+x
2-x)
≤
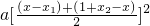
=
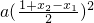
,
∵|x
1|+|x
2|=x
2-x
1=1,
∴
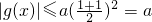
.
分析:(1)由x
1,x
2是f(x)=
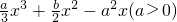
的两个极值点,知x
1,x
2是f′(x)=ax
2+bx-a
2的两个根,由此入手能够证明0<a≤

.
(2)由x
12+x
22+2|x
1x
2|=1,知b
2=(1-4a)a
2,令h(a)=(1-4a)a
2=-4a
3+a
2,得到h′(x)=-2a(6a-1).由此能够证明|b|≤
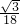
.
(3)g(x)=f′(x)-a(x-x
1)(x-x
2)-a(x-x
1)(x-x
2-1),由x-x
1>0,x
1x
2=-a<0,x
1<0,知x
2>0,x<1,x-x
2-1<0,由此能够证明|g(x)|≤a.
点评:本题考查导数在最大值、最小值中的应用,解题时要认真审题,仔细解答,注意合理地进行等价转化.

 x3+
x3+ x2-a2x(a>0)的两个极值点,且|x1|+|x2|=1.
x2-a2x(a>0)的两个极值点,且|x1|+|x2|=1. ;
;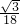 ;
;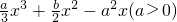 的两个极值点,
的两个极值点,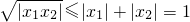 ,
,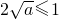 ,
,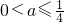 .…(5分)
.…(5分)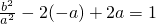 ,
,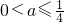 ,
,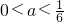 时,h′(a)>0;
时,h′(a)>0;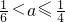 时,h′(a)<0.
时,h′(a)<0. 处取得最大值
处取得最大值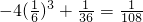 ,
,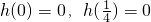 ,
, ]上的最大值为
]上的最大值为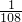 ,
, ]上的最大值为
]上的最大值为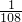 ,此时a=
,此时a= ,
,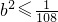 ,即|b|≤
,即|b|≤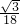 . …(10分)
. …(10分)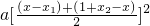
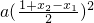 ,
,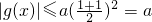 .
.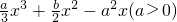 的两个极值点,知x1,x2是f′(x)=ax2+bx-a2的两个根,由此入手能够证明0<a≤
的两个极值点,知x1,x2是f′(x)=ax2+bx-a2的两个根,由此入手能够证明0<a≤ .
.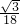 .
.
