
分析 由题意,连接AC交BD于H,则AC⊥平面PDB,连接PH,则∠CPH是直线PC与平面PDB所成的角,求出四棱锥P-ABCD的外接球的半径,即可求出四棱锥P-ABCD的外接球的表面积.
解答 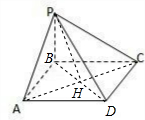 解:由题意,连接AC交BD于H,则AC⊥平面PDB,
解:由题意,连接AC交BD于H,则AC⊥平面PDB,
连接PH,则∠CPH是直线PC与平面PDB所成的角,即∠CPH=30°,
∵CH=$\sqrt{2}$,
∴PC=2$\sqrt{2}$,
∴PD=2$\sqrt{3}$,
∴四棱锥P-ABCD的外接球的半径为$\sqrt{3}$,
∴四棱锥P-ABCD的外接球的表面积为4πR2=12π.
故答案为:12π.
点评 本题考查四棱锥P-ABCD的外接球的表面积,考查线面角,考查学生的计算能力,确定四棱锥P-ABCD的外接球的半径是关键.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{13}$ | C. | $\sqrt{15}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
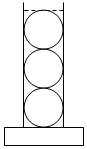 如图,圆柱形容器内盛有高度为6cm的水,若放入3个相同的铁球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球,则球的半径为( )
如图,圆柱形容器内盛有高度为6cm的水,若放入3个相同的铁球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球,则球的半径为( )| A. | 4cm | B. | 3cm | C. | 2cm | D. | 1 cm |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,等腰梯形ABCD中,AB∥CD,DE⊥AB于E,CF⊥AB于F,且AE=BF=EF=2,DE=CF=2.将△AED和△BFC分别沿DE,CF折起,使A,B两点重合,记为点M,得到一个四棱锥M-CDEF,点G,N,H分别是MC,MD,EF的中点.
如图,等腰梯形ABCD中,AB∥CD,DE⊥AB于E,CF⊥AB于F,且AE=BF=EF=2,DE=CF=2.将△AED和△BFC分别沿DE,CF折起,使A,B两点重合,记为点M,得到一个四棱锥M-CDEF,点G,N,H分别是MC,MD,EF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{14}$ | B. | $\sqrt{14}$ | C. | $\sqrt{26}$ | D. | -$\sqrt{26}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 506 | D. | 507 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 赞成禁放 | 不赞成禁放 | 合计 | |
| 老年人 | 60 | 140 | 200 |
| 中青年人 | 80 | 120 | 200 |
| 合计 | 140 | 260 | 400 |
| P(k2>k0) | 0.050 | 0.025 | 0.010 |
| k0 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com