练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设函数f(x)满足x2f′(x)＋2xf(x)＝，f(2)＝，则x＞0时，f(x)(　　)

    A．有极大值，无极小值

    B．有极小值，无极大值

    C．既有极大值又有极小值

    D．既无极大值也无极小值

     

    D

    【解析】由x2f′(x)＋2xf(x)＝，

    得f′(x)＝，

    令g(x)＝ex－2x2f(x)，x＞0，

    则g′(x)＝ex－2x2f′(x)－4xf(x)＝ex－2·＝.

    令g′(x)＝0，得x＝2.

    当x＞2时，g′(x)＞0；当0＜x＜2时，g′(x)＜0，

    ∴g(x)在x＝2时有最小值g(2)＝e2－8f(2)＝0，

    从而当x＞0时，f′(x)≥0，

    则f(x)在(0，＋∞)上是增函数，

    所以函数f(x)无极大值，也无极小值．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014年高考数学考前复习冲刺穿插滚动练习（五）（解析版） 题型：解答题

    设函数f(x)＝sin xcos x－cos(π＋x)cos x(x∈R)．

    (1)求f(x)的最小正周期；

    (2)若函数y＝f(x)的图象按b＝平移后得到函数y＝g(x)的图象，求y＝g(x)在[0，]上的最大值．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学考前复习冲刺穿插滚动练习（三）（解析版） 题型：解答题

    已知向量m＝(sin 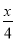，1)，n＝(cos ，cos2)．记f(x)＝m·n．

    (1)若f(α)＝，求cos(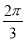－α)的值；

    (2)在△ABC中，角A、B、C的对边分别是a、b、c，且满足(2a－c)cos B＝bcos C，若f(A)＝，试判断△ABC的形状．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学考前复习冲刺穿插滚动练习（三）（解析版） 题型：选择题

    函数f(x)＝ax＋logax在区间[1,2]上的最大值与最小值之和为－，最大值与最小值之积为－，则a的值为(　　)

    A． B． C．2 D．3

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学考前复习冲刺穿插滚动练习（一）（解析版） 题型：解答题

    设集合A＝{x|x2<4}，B＝{x|1<}．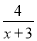

    (1)求集合A∩B；

    (2)若不等式2x2＋ax＋b<0的解集为B，求a，b的值．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学考前复习冲刺穿插滚动练习（一）（解析版） 题型：选择题

    已知f(x)＝ax－2，g(x)＝loga|x|(a>0，且a≠1)，且f(2 011)·g(－2 011)<0，则y＝f(x)，y＝g(x)在同一坐标系内的大致图象是 (　　)

     

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学人教版评估检测 第四章平面向量、数系扩充与复数引入（解析版） 题型：解答题

    (2014·大庆模拟)已知向量a=(,cosωx),b=(sinωx,1),函数f(x)=a·b,且最小正周期为4π.

    (1)求ω的值.

    (2)设α,β∈,f=,f=-,求sin(α+β)的值.

    (3)若x∈[-π,π],求函数f(x)的值域.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学人教版评估检测 第四章平面向量、数系扩充与复数引入（解析版） 题型：选择题

    (2014·宜昌模拟)设P是△ABC所在平面内的一点,若+=2,则(　　)

    A.+=0 B.+=0

    C.+=0 D.++=0

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学人教版评估检测 第六章 不等式、推理与证明（解析版） 题型：选择题

    (2013·西安模拟)已知x>0,y>0,lg2x+lg8y=lg2,则+的最小值是(　　)

    A.2 B.2 C.4 D.2

     

    查看答案和解析>>

    同步练习册答案