Question

8．已知∵f（x）=x²，g（x）=|x-1|，令f₁（x）=g（f（x）），f_n+1（x）=g（f_n（x）），则方程f₂₀₁₅（x）=1解的个数为2017．

Answer 1

分析 根据条件，可求出${f}_{1}（x）=|{x}^{2}-1|$，可画出f₁（x）的图象，根据图象便可看出f₁（x）=1的解有3个，同样可画出f₂（x），f₃（x），的图象，根据图象便可看出f₂（x）=1的解有4个，f₃（x）=1的解有5个，从而便可得出f₂₀₁₅（x）=1解的个数．

解答 解：f（x）=x²，g（x）=|x-1|；
∴①n=0时，${f}_{1}（x）=g（{x}^{2}）=|{x}^{2}-1|$，画出f₁（x）的图象如下：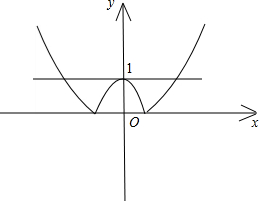
由图看出f₁（x）=1的解有3个；
②n=1时，${f}_{2}（x）=g（|{x}^{2}-1|）=||{x}^{2}-1|-1|$，图象如下：

由图象看出f₂（x）=1的解有4个；
同样的方法可求出f₃（x）=1的解有5个，f₄（x）=1的解有6个；
∴f₂₀₁₅（x）=1的解有2+2015=2017个．
故答案为：2017．

点评 考查二次函数图象，清楚f（x）图象和|f（x）|图象的关系，根据函数图象求方程解的个数的方法．