设m>3,对于项数为m的有穷数列{an},令bk为a1,a2,a3…ak(k≤m)中的最大值,称数列{bn}为{an}的“创新数列”.例如数列3,5,4,7的创新数列为3,5,5,7.考查自然数1、2…m(m>3)的所有排列,将每种排列都视为一个有穷数列{cn}.
(Ⅰ)若m=5,写出创新数列为3,5,5,5,5的所有数列{cn};
(Ⅱ)是否存在数列{cn}的创新数列为等比数列?若存在,求出符合条件的创新数列;若不存在,请说明理由;
(Ⅲ)是否存在数列{cn},使它的创新数列为等差数列?若存在,求出所有符合条件的数列{cn}的个数;若不存在,请说明理由.
【答案】
分析:(I)由题意可得,创新数列为3,4,4,4的所有数列{c
n}有两,即3,4,1,2和3,4,2,1.
(II)设数列{c
n}的创新数列为{e
n},因为e
m为前m个自然数中最大的一个,所以e
m=m,经检验,只有公比q=1时,数列{c
n}才有唯一的一个创新数列.
(III)设存在数列{c
n},使它的创新数列为等差数列,当d=0时,{e
m}为常数列,满足条件;数列{c
n}是首项为m的任意一个排列,共有
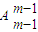
个数列.当d=1时,符合条件的数列{e
m}只能是1,2,3…m,此时数列{c
n}是1,2,3…m,有1个.d≥2时,{e
m} 不存在.由此得出结论.
解答:解:(I)根据“创新数列”的定义,可得创新数列为3,5,5,5,5的数列{c
n}有:
3,5,1,2,4.
3,5,1,4,2.
3,5,2,1,4.
3,5,2,4,1.
3,5,4,1,2.
3,5,4,2,1.…(4分)
(II)存在数列{c
n}的创新数列为等比数列.…(5分)
设数列{c
n}的创新数列为{e
n},因为e
m为前m个自然数中最大的一个,所以e
m=m. …(6分)
若{e
m}为等比数列,设公比为q,因为 e
k+1≥e
k (k=1,2,3…m-1),所以q≥1.…(7分)
当q=1时,{e
m}为常数列满足条件,即为数列为常数数列,每一项都等于m. …(9分)
当q>1时,{e
m}为增数列,符合条件的数列只能是1,2,3…m,
又1,2,3…m不满足等比数列,综上符合条件的创新数列只有一个. …(10分)
(3)设存在数列{c
n},使它的创新数列为等差数列,…(11分)
设数列{c
n}的创新数列为{e
m},因为e
m为前m个自然数中最大的一个,所以e
m=m.若 {e
m}为等差数列,设公差为d,
因为 e
k+1≥e
k (k=1,2,3…m-1),所以 d≥0.且d∈N
*. …(12分)
当d=0时,{e
m}为常数列,满足条件,即为数列 e
m=m,
此时数列{c
n}是首项为m的任意一个排列,共有
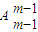
个数列; …(14分)
当d=1时,符合条件的数列{e
m}只能是1,2,3…m,此时数列{c
n}是1,2,3…m,有1个; …(15分)
当d≥2时,∵e
m=e
1+(m-1)d≥e
1+2(m-1)=e
1+m+m-2 又 m>3,∴m-2>0.
∴e
m>m 这与 e
m=m矛盾,所以此时{e
m} 不存在. …(17分)
综上满足条件的数列{c
n}的个数为(m-1)!+1个. …(18分)
点评:本题主要考查等差关系的确定,等比关系的确定,创新数列的定义,属于中档题.

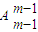 个数列.当d=1时,符合条件的数列{em}只能是1,2,3…m,此时数列{cn}是1,2,3…m,有1个.d≥2时,{em} 不存在.由此得出结论.
个数列.当d=1时,符合条件的数列{em}只能是1,2,3…m,此时数列{cn}是1,2,3…m,有1个.d≥2时,{em} 不存在.由此得出结论.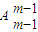 个数列; …(14分)
个数列; …(14分)

 ABC考王全优卷系列答案
ABC考王全优卷系列答案