
分析 (1)设圆柱的半径为r,由$\frac{r}{2}=\frac{6-x}{6}⇒r=\frac{6-x}{3}$,又l=x(0<x<6),可得圆柱侧面积,利用配方法求出最大值.
(2)利用选择结构,写出算法并画出程序框图.
解答 解:(1)设圆柱的半径为r,由$\frac{r}{2}=\frac{6-x}{6}⇒r=\frac{6-x}{3}$,又l=x(0<x<6)
所以${S_{圆柱侧}}=2π•\frac{6-x}{3}•x=\frac{-2π}{3}[{(x-3)^2}-9](0<x<6)$(未注明定义域扣2分)
当且仅当x=3时,${({S_{圆柱侧}})_{max}}=6πc{m^2}$
(2)算法步骤如下:
第一步:输入三个数a,b,c;
第二步:把a赋给x;
第三步:若x>b,则执行第四步,否则把b赋给x;
第四步:若x>c,则执行第五步,否则把c赋给x;
第五步:输出x,结束算法.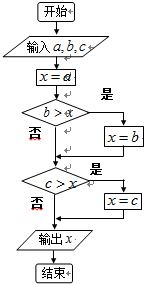
点评 本题考查圆柱侧面积,考查算法知识,考查学生分析解决问题的能力,综合性强.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,$\sqrt{2}$) | B. | (-$\sqrt{2}$,$\sqrt{2}$) | C. | (-$\sqrt{2}$,-1] | D. | [-1,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
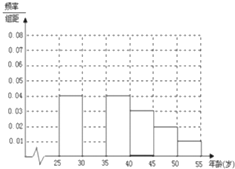 某班同学参加社会实践活动,对本市25~55岁年龄段的人群进行某项随机调查,得到各年龄段被调查人数的频率分布直方图如右(部分有缺损):
某班同学参加社会实践活动,对本市25~55岁年龄段的人群进行某项随机调查,得到各年龄段被调查人数的频率分布直方图如右(部分有缺损):查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{160π}{3}$ | B. | $\frac{59π}{6}$ | C. | $\frac{325π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com