
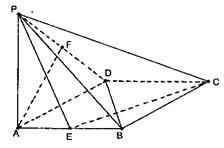
如图,已知:在菱形ABCD中,∠DAB=60°,PA⊥底面ABCD,PA=AB=2,E,F分别是AB与PD的中点.
(1)求证:PC⊥BD;
(2)求证:AF//平面PEC;
(3)求二面角P—EC—D的大小.
(1)证明见解析(2)证明见解析(3)![]()
证明:(1)连结AC,则AC⊥BD。
∵PA⊥平面ABCD,AC是斜线PC在平面ABCD上的射影,
∴由三垂线定理得PC⊥BD。………………4分
(2)取PC的中点K,连结FK、EK,则四边形AEKF是平行四边形。
∴AF//EK,又EK![]() 平面PEC,AF
平面PEC,AF![]() 平面PEC,∴AF//平面PEC。…………4分
平面PEC,∴AF//平面PEC。…………4分
(3)延长DA、CE交于M,过A作AH⊥CM于H,
连结PH,由于PA⊥平面ABCD,可得PH⊥CM。
∴∠PHA为所求二面角P—EC—D的平面角。………………10分
∵E为AB的中点,AE//CD,∴AM=AD=2,
在△AME中,∠MAE=120°,
由余弦定理得![]()
![]()
![]()
![]() ………………14分
………………14分


 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
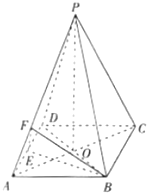 如图,已知四棱锥P-ABCD的底面积是菱形,AC交BD于O,PO⊥平面ABC,E为AD中点,F在PA上,AP=λAF,PC∥平面BEF.
如图,已知四棱锥P-ABCD的底面积是菱形,AC交BD于O,PO⊥平面ABC,E为AD中点,F在PA上,AP=λAF,PC∥平面BEF.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知二次函数y=x2-2x-1的图象的顶点为A.二次函数y=ax2+bx的图象与x轴交于原点O及另一点C,它的顶点B在函数y=x2-2x-1的图象的对称轴上.
如图,已知二次函数y=x2-2x-1的图象的顶点为A.二次函数y=ax2+bx的图象与x轴交于原点O及另一点C,它的顶点B在函数y=x2-2x-1的图象的对称轴上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
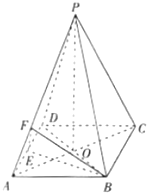 如图,已知四棱锥P-ABCD的底面积是菱形,AC交BD于O,PO⊥平面ABC,E为AD中点,F在PA上,AP=λAF,PC∥平面BEF.
如图,已知四棱锥P-ABCD的底面积是菱形,AC交BD于O,PO⊥平面ABC,E为AD中点,F在PA上,AP=λAF,PC∥平面BEF.查看答案和解析>>
科目:高中数学 来源:2011-2012学年云南省昆明一中高三(上)第二次摸底数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2012-2013学年北京市东城区示范校高三(上)12月联考数学试卷(文科)(解析版) 题型:选择题
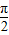 ),则四棱锥P-ABCD的体积V的取值范围是( )
),则四棱锥P-ABCD的体积V的取值范围是( )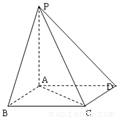
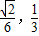 )
)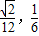 ]
] ]
]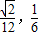 )
)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com