
����Ŀ��Ϊ���˽�¸߶�����������״��,ij�����Ը߶��꼶����������(��λ: ![]() )�����˳�������,�õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ.��֪������
)�����˳�������,�õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ.��֪������![]() ֮�������������������
֮�������������������![]() ֮���������1��.
֮���������1��.
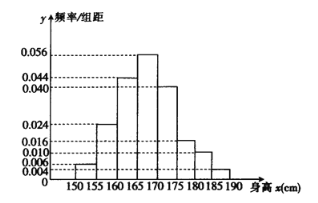
(1)��������![]() ���ڵĶ���Ϊ��������,���õ������и߶�����18000��,��õ����߶����������������Ĵ�Լ�ж�����?
���ڵĶ���Ϊ��������,���õ������и߶�����18000��,��õ����߶����������������Ĵ�Լ�ж�����?
(2)������ȡ��������������![]() ��
��![]() �������������ѡ��2�˵�����ƽʱ��������ϰ�߶����ߵ�Ӱ��,����ѡ����2����������һ�����ߴ���185
�������������ѡ��2�˵�����ƽʱ��������ϰ�߶����ߵ�Ӱ��,����ѡ����2����������һ�����ߴ���185![]() �ĸ����Ƕ���?
�ĸ����Ƕ���?
���𰸡�(1)12600��(2) ![]() .
.
��������
��1����Ƶ�ʷֲ�ֱ��ͼ֪������������Ƶ�ʣ����ǿɵô𰸣�
��2���ȼ�����������������ҳ�������������![]() �е��������Ӷ����ùŵ����ʽ�õ���.
�е��������Ӷ����ùŵ����ʽ�õ���.
��1����Ƶ�ʷֲ�ֱ��ͼ֪������������Ƶ��Ϊ0.7�����Թ������壬���õ������и߶��꼶����������������Ƶ��Ϊ0.7�����Ըõ����߶����������������Ĵ�Լ��![]() ��.
��.
��2��������ȡ������������![]() ��Ƶ��Ϊ
��Ƶ��Ϊ![]() ����֪������
����֪������![]() ��Ƶ��Ϊ
��Ƶ��Ϊ![]() ��������������Ϊ
��������������Ϊ![]() ����������������
����������������![]() �е���3�ˣ���Ϊ
�е���3�ˣ���Ϊ![]() ��������
��������![]() �е���2�ˣ���Ϊ
�е���2�ˣ���Ϊ![]() ������5������ѡ2�ˣ�����
������5������ѡ2�ˣ�����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() 10�ֲ�ͬ��ѡ��������ÿ��ѡ�����ǻ����ҵȿ��ܵģ����ԣ���ѡ2����������һ�����ߴ���185
10�ֲ�ͬ��ѡ��������ÿ��ѡ�����ǻ����ҵȿ��ܵģ����ԣ���ѡ2����������һ�����ߴ���185![]() �ĸ���
�ĸ���![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��ί����֯ij����С��Ϊ��λ������ĩʱ�����һ�����ʵ�����ÿ��С����5��ͬѧ���ڻ������ѧУ��ί��Ըð������ͬѧ�����˲��ԣ��ð��A��B����С������ͬѧ�÷֣��ٷ��ƣ��ľ�Ҷͼ��ͼ��ʾ������B��һͬѧ�ķ����ѱ����𣬵�֪��B��ѧ����ƽ���ֱ�A��ͬѧ��ƽ���ָ�һ�֣�
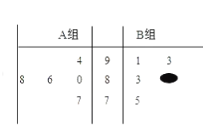
��1������B��ѧ���������ѡ1�ˣ�����÷ֳ���86�ֵĸ��ʣ�
��2���ִ�A��B����ѧ���зֱ������ȡ1��ͬѧ����������ֱ�Ϊm��n����![]() �ĸ��ʣ�
�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijһ�������ĸ�����Ԫ������ͼ��ʽ���Ӷ��ɣ�Ԫ��1��Ԫ��2������������Ԫ��3��Ԫ��4��������������������.���ĸ�����Ԫ����ʹ����������λ��Сʱ����������̬�ֲ�![]() ���Ҹ���Ԫ���ܷ������������������ô�ò�����ʹ����������1000Сʱ�ĸ���Ϊ__________��
���Ҹ���Ԫ���ܷ������������������ô�ò�����ʹ����������1000Сʱ�ĸ���Ϊ__________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���A��B��C���Եı߷ֱ�Ϊa��b��c����SΪ��ABC�����������S��![]() ��a2+c2��b2����
��a2+c2��b2����
��1�����B�Ĵ�С��
��2������b��![]() ����a+c��ȡֵ��Χ��
����a+c��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У����ӵ�M�������ݡ��᷽���N����һ·����ΪM��N��һ����L·��������ͼ��ʾ��·��MM1M2M3N��·��MN1N����M��N�ġ�L·������ij���������½����������ֱ�λ��ƽ��xOy������A��3��20����B����10��0����C��14��0�������ּƻ���x���Ϸ�������x�ᣩ�ڵ�ijһ��P����һ���Ļ����ģ�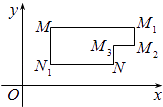
��1��д����P��������A�ġ�L·����������Сֵ�ı���ʽ����Ҫ��֤������
��2������ԭ��OΪԲ�ģ��뾶Ϊ1��Բ���ڲ��DZ���������L·�������ܽ��뱣��������ȷ����P��λ�ã�ʹ�䵽�����������ġ�L·��������֮����С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ȫ��ΪR������A={x|�� ![]() ��x��1}��B={x|x2��6x+8��0}����A�ɣ�RB��=�� ��
��x��1}��B={x|x2��6x+8��0}����A�ɣ�RB��=�� ��
A.{x|x��0}
B.{x|2��x��4}
C.{x|0��x��2��x��4}
D.{x|0��x��2��x��4}
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�������
�У�������![]() �Ľ���Ϊ
�Ľ���Ϊ![]() ����
����![]() ��������
��������![]() ��һ�㣬��
��һ�㣬��![]() ��
��
��1����![]() ��ֵ��
��ֵ��
��2����![]() ������
������![]() ������
������![]() �����㣬��
�����㣬��![]() ���ǵ�
���ǵ�![]() ��ֱ��
��ֱ��![]() �ľ���ֱ�Ϊ
�ľ���ֱ�Ϊ![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����еĸ�˰���������涨����˰��������ԭ����2000Ԫ��ߵ�3500Ԫ�����������µĸ�������˰˰�ʱ���
ȫ��Ӧ��˰���ö� | ˰�� |
������1500Ԫ�IJ��� | 3% |
����1500Ԫ��4500Ԫ�IJ��� | 10% |
����4500Ԫ��9000Ԫ�IJ��� | 20% |
����9000Ԫ��35000Ԫ�IJ��� | 25% |
���� | �� |
����ij�˵��¹�������Ϊ5000Ԫ����ô��Ӧ�ɸ�������˰Ϊ��![]() ��Ԫ��.
��Ԫ��.
���������¹�������Ϊ6000Ԫ�����Ӧ�ɵĸ����յ�˰��
�������ҵ��¹�������Ϊ![]() Ԫ��Ӧ�ɸ�������˰Ϊ
Ԫ��Ӧ�ɸ�������˰Ϊ![]() Ԫ����
Ԫ����![]() ����
����![]() �����
�����
��������ij��Ӧ�ɵĸ�������˰Ϊ1000Ԫ�����������¹�������.�����۲�Ҫ��֤����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com