练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知f(x)=a1x+a2x2+a3x3+…+anxn,且a1,a2,a3,…,an组成等差数列(n为正偶数),又f(1)=n2,f(-1)=n.

    (1)求数列的公差d;

    (2)比较f()与3的大小,并说明理由.

    解：(1)f(1)=a1+a2+…+an=,

    ∴a1+an=2n,2a1+(n-1)d=2n.

    又f(-1)=-a1+a2-a3+a4-…+(-1)nan=n,

    ∴,d=2,a1=1.

    (2)∵f(x)=x+3x2+5x3+…+(2n-1)xn,

    ∴f()=+3()2+5()3+…+(2n-1)()n,                  ①

    f()=()2+3()3+5()4+…+(2n-3)()n+(2n-1)()n+1.    ②

    2×(①-②)得

    =1+2--(2n-1)·＜3.

    ∴f()＜3.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知f(x)=a1x+a2x2+a3x3+……＋anxn ,n为正偶数，且a1 ,a2 ,a3, ……,

    an组成等差数列，又f(1)=n2 ,f(-1)=n ，试比较f( )与3的大小

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知f(x)=a1x+a2x2+…+anxn,且a1,a2,…,an组成等差数列(n为正偶数).又f(1)=n2,f(-1)=n.

    (1)求数列{an}的通项公式;

    (2)证明＜f()＜3(n＞2).

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知f(x)=a1x+a2x2+a3x3+…+anxn，且a1，a2，a3，…，an组成等差数列，n为正偶数，又f(1)=n2，f(-1)=n．

    a1

    a2    a3

    a4    a5    a6

    a7    a8    a9    a10

    (1)求数列{an}的通项公式；

    (2)将数列{an}的各项排成三角形状(如图)，记A(i，j)为第i行第j个数，例如：A(4，3)=a9，求A(10，1)+A(10，2)+…+A(10，10)；

    (3)若bn=,cn=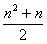,Tn为数列{cn}的前n项和，若Tn＜λ(bn+1+1)，对一切n∈N*都成立，试求λ的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

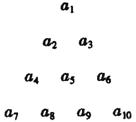
    已知f(x)=a1x+a2x2+a3x3+…+anxn，且al，a2，a3，…，an组成等差数列，n为正偶数，又f(1)=n2，f(-1)=n．

    (1)求数列{an}的通项公式；

    (2)将数列{an}的各项排成三角形状(如图)，记A(i，j)为第i行第j个数，例如：A(4，3)=a9，求A(10，1)+A(10，2)+…+A(10，10)；

    (3)比较f()与3的大小.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    (理)已知函数f(x)=ln(x+)+，g(x)=lnx．

    (1)求函数f(x)的单调区间；

    (2)如果关于x的方程g(x)=x+m有实数根，求实数m的取值范围；

    (3)是否存在正数k，使得关于x的方程f(x)=kg(x)有两个不相等的实数根?如果存在，求k满足的条件；如果不存在，说明理由．

    (文)已知f(x)=a1x+a2x2+a3x3+…+anxn(n∈N*)满足f(1)=n2．

    (1)求数列{an}的通项公式，并指出数列为何数列；

    (2)求证：＜f()＜3(n＞2，n∈N*)．

    查看答案和解析>>

    同步练习册答案