
| A. | 向左平行平移$\frac{π}{2}$个单位长度 | B. | 向右平行平移$\frac{π}{4}$个单位长度 | ||
| C. | 向右平行平移$\frac{π}{2}$个单位长度 | D. | 向左平行平移$\frac{π}{4}$个单位长度 |
分析 利用y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:∵y=2sin(2x-$\frac{π}{3}$)=2sin2(x-$\frac{π}{6}$),y=2sin(2x+$\frac{π}{6}$)=2sin2(x+$\frac{π}{12}$),$\frac{π}{12}$-(-$\frac{π}{6}$)=$\frac{π}{4}$,
故把函数y=2sinx(2x+$\frac{π}{6}$)的图象上所有的点,向右平行平移$\frac{π}{4}$个单位长度,
可得y=2sin[2(x-$\frac{π}{4}$)+$\frac{π}{6}$=2sin(2x-$\frac{π}{3}$)的图象,
故选:B.
点评 本题主要考查y=Asin(ωx+φ)的图象变换规律,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 因为f(0)?f(2)>0,所以f(x)在(0,2)内没有零点 | |
| B. | 因为1是f(x)的一个零点,所以f(0)?f(2)<0 | |
| C. | 由于f(x)在区间(-∞,0)上单调递减,所以f(x)在(-∞,0)内有唯一的一个零点 | |
| D. | 以上说法都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
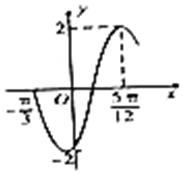 已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示.
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
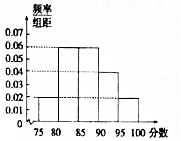 某校为了了解高三学生体育达标情况,在高三学生体育达标成绩中随机抽取50个进行调研,按成绩分组:第l组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示:若要在成绩较高的第3,4,5组中用分层抽样抽取6名学生进行复查:
某校为了了解高三学生体育达标情况,在高三学生体育达标成绩中随机抽取50个进行调研,按成绩分组:第l组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示:若要在成绩较高的第3,4,5组中用分层抽样抽取6名学生进行复查:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{3}}{3}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $a+\frac{1}{b}>b+\frac{1}{a}$ | B. | $\frac{1}{{a{b^2}}}>\frac{1}{{{a^2}b}}$ | C. | $\frac{1}{a}<\frac{1}{b}$ | D. | ab>b2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com