练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

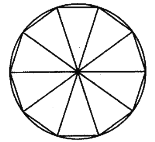
    【题目】在3世纪中期，我国古代数学家刘徽在《九章算术注》中提出了割圆术：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆合体，而无所失矣”.这可视为中国古代极限观念的佳作.割圆术可以视为将一个圆内接正边形等分成个等腰三角形(如图所示)，当变得很大时，等腰三角形的面积之和近似等于圆的面积.运用割圆术的思想，可得到sin3°的近似值为（ ）(取近似值3.14)

    A.0.012B.0.052

    C.0.125D.0.235

    【答案】B

    【解析】

    根据题意圆内接正120边形其等分成120个等腰三角形，每个等腰三角形的顶角为,根据等腰三角形的面积之和近似等于圆的面积.即可列出等式解出sin3°的近似值.

    当时,每个等腰三角形的顶角为,则其面积为,

    又因为等腰三角形的面积之和近似等于圆的面积,

    所以,

    故选：B

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

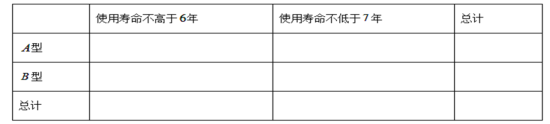
    【题目】2020年春季，某出租汽车公司决定更换一批新的小汽车以代替原来报废的出租车，现有采购成本分别为万元/辆和万元/辆的两款车型，根据以往这两种出租车车型的数据，得到两款出租车车型使用寿命频数表如下：

    （1）填写下表，并判断是否有的把握认为出租车的使用寿命年数与汽车车型有关？

    （2）从和的车型中各随机抽取车，以表示这车中使用寿命不低于年的车数，求的分布列和数学期望；

    （3）根据公司要求，采购成本由出租公司负责，平均每辆出租车每年上交公司万元，其余维修和保险等费用自理.假设每辆出租车的使用寿命都是整数年，用频率估计每辆出租车使用寿命的概率，分别以这辆出租车所产生的平均利润作为决策依据，如果你是该公司的负责人，会选择采购哪款车型？

    附：，.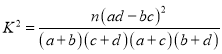

    0.050

    0.010

    0.001

    3.841

    6.635

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在三棱柱中，侧面为菱形，且，点E，F分别为，的中点.求证：

    （1）平面平面；

    （2）平面.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xOy中，曲线C的参数方程为（为参数），直线，以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系.

    （1）求直线l和曲线C的极坐标方程；

    （2）若直线与直线l相交于点A，与曲线C相交于不同的两点M，N.求的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为加强环境保护，治理空气污染，环境监测部门对某市空气质量进行调研，随机抽查了天空气中的和浓度（单位：），得下表：

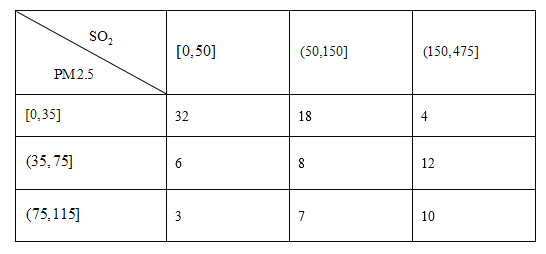
    （1）估计事件“该市一天空气中浓度不超过，且浓度不超过”的概率；

    （2）根据所给数据，完成下面的列联表：

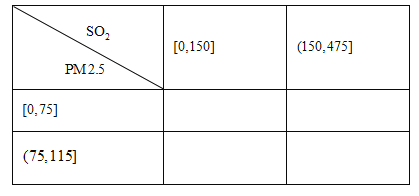
    （3）根据（2）中的列联表，判断是否有的把握认为该市一天空气中浓度与浓度有关？

    附：，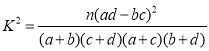

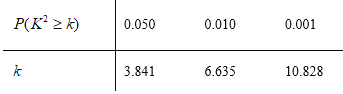
    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，证明.

    （1）存在唯一的极小值点；

    （2）的极小值点为则.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一个正方体的平面展开图如图所示，在这个正方体中，点是棱的中点，，分别是线段，（不包含端点）上的动点，则下列说法正确的是( )

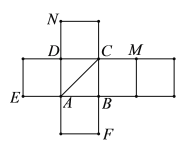
    A.在点的运动过程中，存在

    B.在点的运动过程中，存在

    C.三棱锥的体积为定值

    D.三棱锥的体积不为定值

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的一个顶点为，右焦点为，且，其中为原点．

    （Ⅰ）求椭圆的方程；

    （Ⅱ）已知点满足，点在椭圆上（异于椭圆的顶点），直线与以为圆心的圆相切于点，且为线段的中点．求直线的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】网络购物已经成为人们的一种生活方式．某购物平台为了给顾客提供更好的购物体验，为入驻商家设置了积分制度，每笔购物完成后，买家可以根据物流情况、商品质量等因素对商家做出评价，评价分为好评、中评和差评平台规定商家有50天的试营业时间，期间只评价不积分，正式营业后，每个好评给商家计1分，中评计0分，差评计分，某商家在试营业期间随机抽取100单交易调查了其商品的物流情况以及买家的评价情况，分别制成了图1和图2．

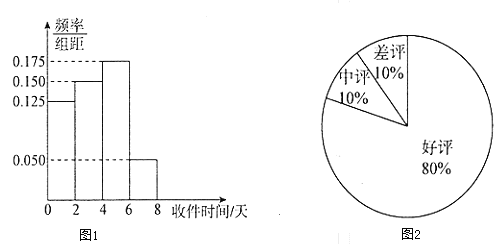
    （1）通常收件时间不超过四天认为是物流迅速，否则认为是物流迟缓；

    请根据题目所给信息完成下面列联表，并判断能否有的把握认为“获得好评”与物流速度有关？

    好评

    中评或差评

    合计

    物流迅速

    物流迟缓

    30

    合计

    （2）从正式营业开始，记商家在每笔交易中得到的评价得分为．该商家将试营业50天期间的成交情况制成了频数分布表（表1），以试营业期间成交单数的频率代替正式营业时成交单数发生的概率．

    表1

    成交单数

    36

    30

    27

    天数

    10

    20

    20

    （Ⅰ）求的分布列和数学期望；

    （Ⅱ）平台规定，当积分超过10000分时，商家会获得“诚信商家”称号，请估计该商家从正式营业开始，1年内（365天）能否获得“诚信商家”称号

    附：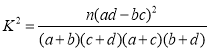

    参考数据：

    0.150

    0．100

    0.050

    0.025

    0.010

    2.072

    2.706

    3.841

    5.024

    6.635

    查看答案和解析>>

    同步练习册答案