
【题目】在直角坐标系xOy中,曲线C的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() ,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系.
,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系.
(1)求直线l和曲线C的极坐标方程;
(2)若直线![]() 与直线l相交于点A,与曲线C相交于不同的两点M,N.求
与直线l相交于点A,与曲线C相交于不同的两点M,N.求![]() 的最小值.
的最小值.
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求证:数列![]() 为等比数列;
为等比数列;
(2)设数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证: ![]() 为定值;
为定值;
(3)判断数列![]() 中是否存在三项成等差数列,并证明你的结论.
中是否存在三项成等差数列,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举办的体育节设有投篮项目.该项目规定:每位同学仅有三次投篮机会,其中前两次投篮每投中一次得1分,第三次投篮投中得2分,若不中不得分,投完三次后累计总分.
(1)若甲同学每次投篮命中的概率为![]() ,且相互不影响,记甲同学投完三次后的总分为X,求随机变量X的概率分布列;
,且相互不影响,记甲同学投完三次后的总分为X,求随机变量X的概率分布列;
(2)若(1)中的甲同学邀请乙同学一起参加投篮项目,已知乙同学每次投篮命中的概率为![]() ,且相互不影响,甲、乙两人之间互不干扰.求甲同学的总分低于乙同学的总分的概率.
,且相互不影响,甲、乙两人之间互不干扰.求甲同学的总分低于乙同学的总分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
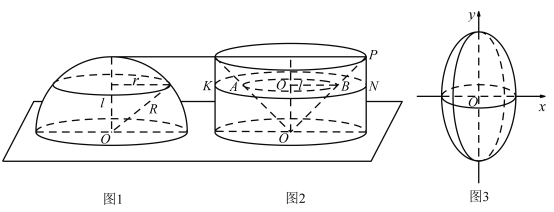
【题目】运用祖暅原理计算球的体积时,夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意一个平面所截,若截面面积都相等,则这两个几何体的体积相等.构造一个底面半径和高都与球的半径相等的圆柱,与半球(如图①)放置在同一平面上,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥后得到一新几何体(如图②),用任何一个平行于底面的平面去截它们时,可证得所截得的两个截面面积相等,由此可证明新几何体与半球体积相等.现将椭圆![]() 绕y轴旋转一周后得一橄榄状的几何体(如图③),类比上述方法,运用祖暅原理可求得其体积等于( )
绕y轴旋转一周后得一橄榄状的几何体(如图③),类比上述方法,运用祖暅原理可求得其体积等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
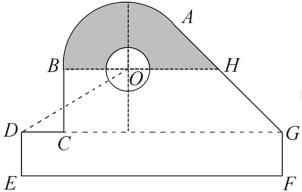
【题目】某中学开展劳动实习,学生加工制作零件,零件的截面如图所示.O为圆孔及轮廓圆弧AB所在圆的圆心,A是圆弧AB与直线AG的切点,B是圆弧AB与直线BC的切点,四边形DEFG为矩形,BC⊥DG,垂足为C,tan∠ODC=![]() ,
,![]() ,EF=12 cm,DE=2 cm,A到直线DE和EF的距离均为7 cm,圆孔半径为1 cm,则图中阴影部分的面积为________cm2.
,EF=12 cm,DE=2 cm,A到直线DE和EF的距离均为7 cm,圆孔半径为1 cm,则图中阴影部分的面积为________cm2.
查看答案和解析>>
科目:高中数学 来源: 题型:
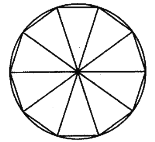
【题目】在3世纪中期,我国古代数学家刘徽在《九章算术注》中提出了割圆术:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”.这可视为中国古代极限观念的佳作.割圆术可以视为将一个圆内接正![]() 边形等分成
边形等分成![]() 个等腰三角形(如图所示),当
个等腰三角形(如图所示),当![]() 变得很大时,等腰三角形的面积之和近似等于圆的面积.运用割圆术的思想,可得到sin3°的近似值为( )(
变得很大时,等腰三角形的面积之和近似等于圆的面积.运用割圆术的思想,可得到sin3°的近似值为( )(![]() 取近似值3.14)
取近似值3.14)
A.0.012B.0.052
C.0.125D.0.235
查看答案和解析>>
科目:高中数学 来源: 题型:
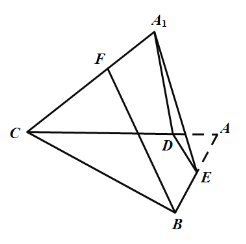
【题目】如图,在边长为4的正三角形![]() 中,E为边
中,E为边![]() 的中点,过E作
的中点,过E作![]() 于D.把
于D.把![]() 沿
沿![]() 翻折至
翻折至![]() 的位置,连结
的位置,连结![]() .翻折过程中,其中正确的结论是( )
.翻折过程中,其中正确的结论是( )
A.![]() ;
;
B.存在某个位置,使![]() ;
;
C.若![]() ,则
,则![]() 的长是定值;
的长是定值;
D.若![]() ,则四面体
,则四面体![]() 的体积最大值为
的体积最大值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数PM2.5(单位:![]() )表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
PM2.5 日均浓度 | 0~35 | 35~75 | 75~115 | 115~150 | 150~250 |
|
空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
空气质量类型 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
甲乙两城市2020年5月份中的15天对空气质量指数PM2.5进行监测,获得PM2.5日均浓度指数数据如茎叶图所示:
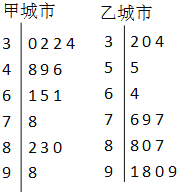
(1)根据你所学的统计知识估计甲乙两城市15天内哪个城市空气质量总体较好?并简要说明理由.
(2)在15天内任取1天,估计甲乙两城市空气质量类别均为优或良的概率;
(3)在乙城市15个监测数据中任取2个,设![]() 为空气质量类别为优或良的天数,求
为空气质量类别为优或良的天数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com