
【题目】空气质量指数PM2.5(单位:![]() )表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
PM2.5 日均浓度 | 0~35 | 35~75 | 75~115 | 115~150 | 150~250 |
|
空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
空气质量类型 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
甲乙两城市2020年5月份中的15天对空气质量指数PM2.5进行监测,获得PM2.5日均浓度指数数据如茎叶图所示:
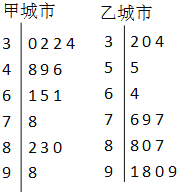
(1)根据你所学的统计知识估计甲乙两城市15天内哪个城市空气质量总体较好?并简要说明理由.
(2)在15天内任取1天,估计甲乙两城市空气质量类别均为优或良的概率;
(3)在乙城市15个监测数据中任取2个,设![]() 为空气质量类别为优或良的天数,求
为空气质量类别为优或良的天数,求![]() 的分布列及数学期望.
的分布列及数学期望.
【答案】(1)甲城市空气质量总体较好,理由见解析;(2)![]() ;(3)分布列见解析,数学期望:
;(3)分布列见解析,数学期望:![]() .
.
【解析】
(1)直接由茎叶图可得结果.
(2)由(1)的分析及相互独立事件的概率计算公式即可得出;
(3)利用超几何分布即可得到分布列,再利用数学期望的计算公式即可得出.
(1)由茎叶图可知:甲城市空气质量一级和二级共有10天,而乙城市空气质量一级和二级只有5天,因此甲城市空气质量总体较好.
(2)甲城市在15天内空气质量类别为优或良的共有10天,任取1天,空气质量类别为优或良的概率为![]() ,
,
乙城市在15天内空气质量类别为优或良的共有5天,任取1天,空气质量类别为优或良的概率为![]() ,
,
在15天内任取1天,估计甲乙两城市空气质量类别均为优或良的概率为![]() .
.
(3)![]() 的取值为0,1,2,
的取值为0,1,2,
![]() ,
,![]() ,
,![]() .
.
![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 |
|
|
|
|
数学期望![]() .
.


科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() ,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系.
,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系.
(1)求直线l和曲线C的极坐标方程;
(2)若直线![]() 与直线l相交于点A,与曲线C相交于不同的两点M,N.求
与直线l相交于点A,与曲线C相交于不同的两点M,N.求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个顶点为
的一个顶点为![]() ,右焦点为
,右焦点为![]() ,且
,且![]() ,其中
,其中![]() 为原点.
为原点.
(Ⅰ)求椭圆的方程;
(Ⅱ)已知点![]() 满足
满足![]() ,点
,点![]() 在椭圆上(
在椭圆上(![]() 异于椭圆的顶点),直线
异于椭圆的顶点),直线![]() 与以
与以![]() 为圆心的圆相切于点
为圆心的圆相切于点![]() ,且
,且![]() 为线段
为线段![]() 的中点.求直线
的中点.求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,以
为极点,以![]() 轴的非负半轴为极轴建立极坐标系,已知曲线
轴的非负半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)过原点![]() 的直线
的直线![]() 与直线
与直线![]() 交于点
交于点![]() ,与曲线
,与曲线![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某口罩厂一年中各月份的收入、支出情况如图所示(单位:万元,下列说法中错误的是(注:月结余=月收入一月支出)( )
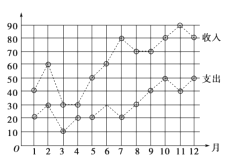
A.上半年的平均月收入为45万元B.月收入的方差大于月支出的方差
C.月收入的中位数为70D.月结余的众数为30
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
, ![]() 为坐标原点,
为坐标原点, ![]() 是双曲线上在第一象限内的点,直线
是双曲线上在第一象限内的点,直线![]() 分别交双曲线
分别交双曲线![]() 左、右支于另一点
左、右支于另一点![]() ,
, ![]() ,且
,且![]() ,则双曲线
,则双曲线![]() 的离心率为( )
的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】网络购物已经成为人们的一种生活方式.某购物平台为了给顾客提供更好的购物体验,为入驻商家设置了积分制度,每笔购物完成后,买家可以根据物流情况、商品质量等因素对商家做出评价,评价分为好评、中评和差评平台规定商家有50天的试营业时间,期间只评价不积分,正式营业后,每个好评给商家计1分,中评计0分,差评计![]() 分,某商家在试营业期间随机抽取100单交易调查了其商品的物流情况以及买家的评价情况,分别制成了图1和图2.
分,某商家在试营业期间随机抽取100单交易调查了其商品的物流情况以及买家的评价情况,分别制成了图1和图2.
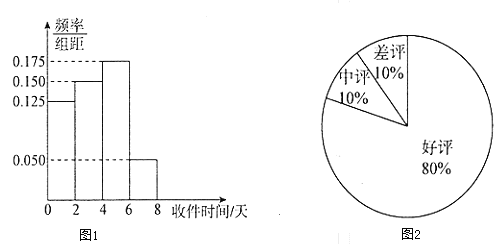
(1)通常收件时间不超过四天认为是物流迅速,否则认为是物流迟缓;
请根据题目所给信息完成下面![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为“获得好评”与物流速度有关?
的把握认为“获得好评”与物流速度有关?
好评 | 中评或差评 | 合计 | |
物流迅速 | |||
物流迟缓 | 30 | ||
合计 |
(2)从正式营业开始,记商家在每笔交易中得到的评价得分为![]() .该商家将试营业50天期间的成交情况制成了频数分布表(表1),以试营业期间成交单数的频率代替正式营业时成交单数发生的概率.
.该商家将试营业50天期间的成交情况制成了频数分布表(表1),以试营业期间成交单数的频率代替正式营业时成交单数发生的概率.
表1
成交单数 | 36 | 30 | 27 |
天数 | 10 | 20 | 20 |
(Ⅰ)求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)平台规定,当积分超过10000分时,商家会获得“诚信商家”称号,请估计该商家从正式营业开始,1年内(365天)能否获得“诚信商家”称号
附: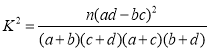
参考数据:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
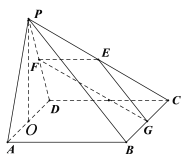
【题目】已知在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 是正三角形,CD平面PAD,E,F,G,O分别是PC,PD,BC,AD 的中点.
是正三角形,CD平面PAD,E,F,G,O分别是PC,PD,BC,AD 的中点.
(Ⅰ)求证:PO平面![]() ;
;
(Ⅱ)求平面EFG与平面![]() 所成锐二面角的大小;
所成锐二面角的大小;
(Ⅲ)线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,若存在,求线段
,若存在,求线段![]() 的长度;若不存在,说明理由.
的长度;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com