
 ?存在唯一的实数λ,使
?存在唯一的实数λ,使 ;
;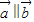 ?存在不全为零的实数λ,μ,使λ
?存在不全为零的实数λ,μ,使λ ;
;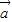 与
与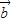 不共线?若存在实数λ,μ使λ
不共线?若存在实数λ,μ使λ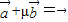 ,则λ=μ=0;
,则λ=μ=0;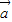 与
与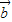 不共线?不存在实数λ,μ使λ
不共线?不存在实数λ,μ使λ .下列命题是真命题的是 (填序号)
.下列命题是真命题的是 (填序号) 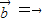 ,
, 时,不存在λ使
时,不存在λ使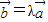 成立,故①为假命题;
成立,故①为假命题;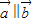 ,分
,分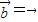 和
和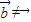 两种情况找λ和μ,结合两个向量平行的条件;
两种情况找λ和μ,结合两个向量平行的条件; ,因为λ、μ不全为0,故
,因为λ、μ不全为0,故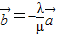 ,故可得
,故可得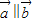 ;
;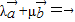 成立.
成立.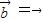 ,
,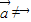 时,不存在λ使
时,不存在λ使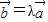 成立,故①为假命题;
成立,故①为假命题; ,
,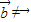 时,由两个向量共线定理知存在实数m,使
时,由两个向量共线定理知存在实数m,使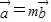 ,取λ=1,μ=-m,则λ、μ不全为0,且
,取λ=1,μ=-m,则λ、μ不全为0,且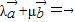 .
.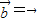 时,取λ=0即可;反之若
时,取λ=0即可;反之若 ,因为λ、μ不全为0,不妨设μ≠0,则
,因为λ、μ不全为0,不妨设μ≠0,则 ,故可得
,故可得 .
.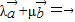 成立,故为假命题.
成立,故为假命题.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| a |
| a |
| ||||
|
| ||
|
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| b |
| a |
| b |
| b |
| a |
| e |
| a |
| e |
| a |
| a |
| e |
| a |
| a |
| a |
| a |
| a |
| b |
| b |
| c |
| a |
| c |
| a |
| b |
| b |
| c |
| b |
| 0 |
| a |
| c |
| OA |
| a |
| OB |
| b |
| a |
| b |
| OM |
| ||
|
|
| ||
|
|
| OM |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| b |
| a |
| e |
| a |
| e |
| a |
| a |
| e |
| a |
| a |
| a |
| a |
| a |
| b |
| b |
| c |
| a |
| c |
| a |
| b |
| b |
| c |
| b |
| 0 |
| a |
| c |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| b |
| a |
| a |
| b |
| c |
| OM |
| 1 |
| 3 |
| OA |
| 1 |
| 3 |
| OB |
| 1 |
| 3 |
| OC |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| b |
| a |
| a |
| b |
| b |
| c |
| a |
| c |
| a |
| b |
| a |
| b |
| 0 |
| a |
| b |
| c |
| b |
| c |
| a |
| c |
| a |
| b |
| c |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| a |
| b |
| x |
| a |
| b |
| y |
| a |
| b |
| x |
| y |
| x |
| y |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com