甲，乙两船同时从
点出发，甲以每小时
的速度向正东航行，乙船以每小时
的速度沿南偏东
的方向航行，
小时后，甲、乙两船分别到达
两点，此时
的大小为 ；
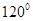
解析试题分析：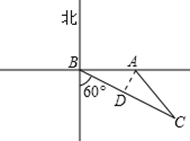
过A作AD⊥BC于D点，∵甲船速度为每小时20km，乙船速度为每小时20
km，且运动的时间是1小时，∴AB=20km，BC=20km，由图形得：∠BAC=30°，∴BD=ABcos30°=10km，∴D为BC的中点，AD垂直平分BC，∴AB=AC=20km，根据余弦定理BC2=AB2+AC2-2AB•AC•cos∠BAC，得：1200=400+400-800cos∠BAC，∴cos∠BAC=-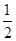
，又∠BAC为三角形的内角，则∠BAC=120°．故答案为：120°
考点：解三角形的运用
点评：此题考查了余弦定理，线段垂直平分线的判定与性质，以及锐角三角形函数定义，利用了数形结合的数学思想，熟练掌握余弦定理是解本题的关键
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
中，角
所对的边分别为
，已知
，
，则
__________
，则△ABC为 三角形；
，
，
，则
等于 。 
中，
，则A的取值范围是 ．
中，AD为BC边上的中线，且AC=2AB=2AD=4,则BD＝________.
中，内角
所对的边分别为
，
，则其外接圆的半径
，那么△ABC是 三角形．(填“钝角”、“锐角”、“直角”)
中，若
，
，则
的最小值是 。