
如图,在直角梯形ABCD中,AD⊥AB,AB∥DC,AD=DC=1,AB=2,动点P在以点C为圆心,且与直线BD相切的圆上或圆内移动,设 =λ
=λ +μ
+μ (λ,μ∈R),则λ+μ的取值范围是( ).
(λ,μ∈R),则λ+μ的取值范围是( ).

A.(1,2) B.(0,3) C.[1,2] D.[1,2)
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练5练习卷(解析版) 题型:选择题
下面四个图象中,有一个是函数f(x)=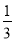 x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)图象,则f(-1)等于( ).
x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)图象,则f(-1)等于( ).
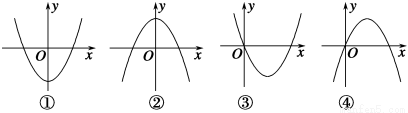
A. 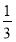 B.-
B.-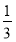 C.
C. 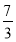 D.-
D.- 或
或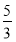
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练1练习卷(解析版) 题型:选择题
已知定义在R上的函数y=f(x)满足以下三个条件:①对于任意的x∈R,都有f(x+4)=f(x);②对于任意的x1,x2∈R,且0≤x1<x2≤2,都有f(x1)<f(x2);③函数y=f(x+2)的图象关于y轴对称.则下列结论中正确的是( ).
A.f(4.5)<f(7)<f(6.5) B.f(7)<f(4.5)<f(6.5)
C.f(7)<f(6.5)<f(4.5) D.f(4.5)<f(6.5)<f(7)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习6-2椭圆、双曲线、抛物线练习卷(解析版) 题型:填空题
已知双曲线 =1(a>0,b>0)的离心率为e=2,过双曲线上一点M作直线MA,MB交双曲线于A,B两点,且斜率分别为k1,k2,若直线AB过原点O,则k1·k2的值为________.
=1(a>0,b>0)的离心率为e=2,过双曲线上一点M作直线MA,MB交双曲线于A,B两点,且斜率分别为k1,k2,若直线AB过原点O,则k1·k2的值为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习6-2椭圆、双曲线、抛物线练习卷(解析版) 题型:选择题
已知双曲线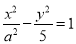 的右焦点为(3,0),则该双曲线的离心率等于( ).
的右焦点为(3,0),则该双曲线的离心率等于( ).
A. 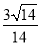 B.
B. 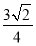 C.
C. 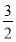 D.
D. 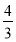
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习5-2空间向量与立体几何练习卷(解析版) 题型:解答题
如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成的角为60°.

(1)求证:AC⊥平面BDE;
(2)求二面角F-BE-D的余弦值;
(3)设点M是线段BD上一个动点,试确定点M的位置,使得AM∥平面BEF,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习5-2空间向量与立体几何练习卷(解析版) 题型:选择题
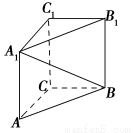
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是( ).
A. 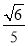 B.
B. 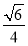 C.
C. 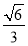 D.
D. 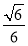
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习4-2数列求和与数列的综合应用练习卷(解析版) 题型:填空题
已知等比数列{an}为递增数列,且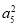 =a10,2(an+an+2)=5an+1,则a2n=________.
=a10,2(an+an+2)=5an+1,则a2n=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习2-2导数及其应用练习卷(解析版) 题型:选择题
设f(x)在R上可导,其导数为f′(x),给出下列四组条件:
①p:f(x)是奇函数,q:f′(x)是偶函数;
②p:f(x)是以T为周期的函数,q:f′(x)是以T为周期的函数;
③p:f(x)在区间(-∞,+∞)上为增函数,q:f′(x)>0在(-∞,+∞)恒成立;
④p:f(x)在x0处取得极值,q:f′(x0)=0.
由以上条件中,能使p⇒q成立的序号为 ( ).
A.①②③ B.①②④ C.①③④ D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com