设f(x)在R上可导，其导数为f′(x)，给出下列四组条件：
①p：f(x)是奇函数，q：f′(x)是偶函数；
②p：f(x)是以T为周期的函数，q：f′(x)是以T为周期的函数；
③p：f(x)在区间(－∞，＋∞)上为增函数，q：f′(x)＞0在(－∞，＋∞)恒成立；
④p：f(x)在x0处取得极值，q：f′(x0)＝0.
由以上条件中，能使p⇒q成立的序号为 ( )．
A．①②③ B．①②④ C．①③④ D．②③④
科目：高中数学 来源：2014年高考数学（理）二轮复习6-1直线与圆练习卷（解析版） 题型：选择题
如图，在直角梯形ABCD中，AD⊥AB，AB∥DC，AD＝DC＝1，AB＝2，动点P在以点C为圆心，且与直线BD相切的圆上或圆内移动，设
＝λ
＋μ
(λ，μ∈R)，则λ＋μ的取值范围是( )．
A．(1,2) B．(0,3) C．[1,2] D．[1,2)
查看答案和解析>>
科目：高中数学 来源：2014年高考数学（理）二轮复习4-1等差数列与等比数列练习卷（解析版） 题型：选择题
设等比数列{an}的公比q＝2，前n项和为Sn，若S4＝1，则S8＝ ( )．
A．17 B.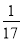 
C．5 D.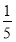 
查看答案和解析>>
科目：高中数学 来源：2014年高考数学（理）二轮复习3-1三角函数与三角恒等变换练习卷（解析版） 题型：填空题
已知函数f(x)＝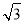
sin ωx＋cos ωx(ω＞0)，y＝f(x)的图象与直线y＝2的两个相邻交点的距离等于π，则f(x)的单调递增区间是________．
查看答案和解析>>
科目：高中数学 来源：2014年高考数学（理）二轮复习2-2导数及其应用练习卷（解析版） 题型：解答题
已知f(x)＝xln x，g(x)＝x3＋ax2－x＋2.
(1)求函数f(x)的单调区间；
(2)求f(x)在区间[t，t＋2](t＞0)上的最小值；
(3)对一切的x∈(0，＋∞)，2f(x)＜g′(x)＋2恒成立，求实数a的取值范围．
查看答案和解析>>
科目：高中数学 来源：2014年高考数学（理）二轮复习2-1函数的概念与基本初等函数练习卷（解析版） 题型：解答题
某养殖厂需定期购买饲料，已知该厂每天需要饲料200千克，每千克饲料的价格为1.8元，饲料的保管费与其他费用平均每千克每天0.03元，购买饲料每次支付运费300元．
(1)求该厂多少天购买一次饲料才能使平均每天支付的总费用最少；
(2)若提供饲料的公司规定，当一次购买饲料不少于5吨时，其价格可享受八五折优惠(即原价的85%)．问：该厂是否应考虑利用此优惠条件？请说明理由．
查看答案和解析>>
科目：高中数学 来源：2014年高考数学（理）二轮复习2-1函数的概念与基本初等函数练习卷（解析版） 题型：选择题
已知函数f(x)是定义在R上的奇函数，且当x＞0时，f(x)＝2x－3，则f(－2)=( )．
A．1 B．－1 C.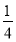 
D．－
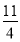
查看答案和解析>>
科目：高中数学 来源：2014年高考数学（理）二轮专题复习知能提升演练选修4-5练习卷（解析版） 题型：填空题
若关于实数x的不等式|x－5|＋|x＋3|<a无解，则实数a的取值范围是________．
查看答案和解析>>
科目：高中数学 来源：2014年高考数学（理）二轮专题复习知能提升演练1-7-3练习卷（解析版） 题型：选择题
通过随机询问110名性别不同的人，对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查，得到如下的列联表：
| 男 | 女 | 总计 |
走天桥 | 40 | 20 | 60 |
走斑马线 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由K2＝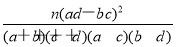
，得K2＝
≈7.8.
附表：
P(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
参照附表，得到的正确结论 ( )．
A．有99%以上的把握认为“选择过马路的方式与性别有关”
B．有99%以上的把握认为“选择过马路的方式与性别无关”
C．在犯错误的概率不超过0.1%的前提下，认为“选择过马路的方式与性别有关”
D．在犯错误的概率不超过0.1%的前提下，认为“选择过马路的方式与性别无关”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
